题目内容

3．（$\sqrt{x}$-$\frac{1}{x}$）9展开式中的常数项是（　　）
A．-84B．84C．-36D．36

分析 利用通项公式即可得出．

解答 解：（$\sqrt{x}$-$\frac{1}{x}$）9展开式中的通项公式：Tr+1=${∁}_{9}^{r}（\sqrt{x}）^{9-r}$$（-\frac{1}{x}）^{r}$=（-1）r${∁}_{9}^{r}$${x}^{\frac{9-3r}{2}}$，
令$\frac{9-3r}{2}$=0，解得r=3．
∴常数项=-${∁}_{9}^{3}$=-84．
故选：A．

点评 本题考查了二项式定理的应用，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
13．设an=xn，bn=（$\frac{1}{n}$）2，Sn为数列{an•bn}的前n项和，令fn（x）=Sn-1，x∈R，a∈N*．
（Ⅰ）若x=2，求数列{$\frac{2n-1}{{a}_{n}}$}的前n项和Tn；
（Ⅱ）求证：对?n∈N*，方程fn（x）=0在xn∈[$\frac{2}{3}$，1]上有且仅有一个根；
（Ⅲ）求证：对?p∈N*，由（Ⅱ）中xn构成的数列{xn}满足0＜xn-xn+p＜$\frac{1}{n}$．
14．如图，圆O是一半径为10米的圆形草坪，为了满足周边市民跳广场舞的需要，现规划在草坪上建一个广场，广场形状如图中虚线部分所示的曲边四边形，其中A，B两点在⊙O上，A，B，C，D恰是一个正方形的四个顶点．根据规划要求，在A，B，C，D四点处安装四盏照明设备，从圆心O点出发，在地下铺设4条到A，B，C，D四点线路OA，OB，OC，OD．
（1）若正方形边长为10米，求广场的面积；
（2）求铺设的4条线路OA，OB，OC，OD总长度的最小值．
11．某三棱锥的三视图如图所示，正视图和俯视图都是等腰直角三角形，则该三棱锥中棱长最大值是（　　）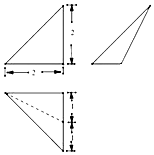
A．$2\sqrt{5}$B．$2\sqrt{3}$C．$2\sqrt{2}$D．$\sqrt{5}$
18．执行如图所示的程序框图，若输入a=5，b=2，则输出n的值为（　　）
A．2B．3C．4D．5
8．二项式${（2x-\frac{a}{{\sqrt{x}}}）^n}$的展开式中所有项二项式系数和为64，则展开式中的常数项为60，则a的值为（　　）
A．2B．±1C．-1D．1
15．若f（n）=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n+1}$（n∈N*），则当n=2时，f（n）是$\frac{137}{60}$．
12．执行若图所示的程序框图，若输入的n=216，则输出s的值为（　　）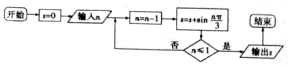
A．$\frac{{\sqrt{3}}}{2}$B．$\sqrt{3}$C．$-\frac{{\sqrt{3}}}{2}$D．0
13．设函数f（x）=|2x-1|．
（Ⅰ）解关于x的不等式f（2x）≤f（x+1）；
（Ⅱ）若实数a，b满足a-2b=2，求f（a+1）+f（2b-1）的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网