题目内容
已知函数f(x)=log
|sinx-cosx|.
(1)求f(x)的定义域和值域;
(2)判断f(x)的奇偶性和周期性;
(3)求f(x)的单调区间.
| 1 |
| 2 |
(1)求f(x)的定义域和值域;
(2)判断f(x)的奇偶性和周期性;
(3)求f(x)的单调区间.
考点:对数函数的图像与性质,两角和与差的正弦函数
专题:函数的性质及应用
分析:(1)令对数的真数大于0求出x的范围为定义域,据三角函数的有界性求出值域.
(2)判断函数的奇偶性先看定义域,定义域关于原点对称是函数具有奇偶性的必要条件据函数最小正周期的定义,求出周期.
(3)函数为复合函数,据符号函数的单调性同增异减,外函数是减函数,求出内函数的递增区间为函数的递减区间;内函数的递减区间为函数的递增区间.
(2)判断函数的奇偶性先看定义域,定义域关于原点对称是函数具有奇偶性的必要条件据函数最小正周期的定义,求出周期.
(3)函数为复合函数,据符号函数的单调性同增异减,外函数是减函数,求出内函数的递增区间为函数的递减区间;内函数的递减区间为函数的递增区间.
解答:
解:(1)由题意得:sinx-cosx≠0,∴x≠kπ+
,
∴函数的定义域为{x|x≠kπ+
},(k∈Z).
由sinx-cosx=
sin(x-
),得0<|sinx-cosx|≤
,
∴f(x)=log
|sinx-cosx|≥-
,
∴函数f(x)的值域是[-
,+∞);
(2)因为f(x)定义域在数轴上对应的点不关于原点对称,故f(x)是非奇非偶函数,
f(x)=
=
=
-
,
∵有绝对值,∴T=
=π;
(3)∵函数y=|sinx-cosx|=
|sin(x-
)|,
由kπ<x-
≤kπ+
,得:kπ+
<x≤kπ+
π,
∴函数y=|sinx-cosx|在(kπ+
,kπ+
π]递增,
由kπ+
≤x-
≤kπ+π,得:kπ+
π≤x≤kπ+
π,
∴函数y=|sinx-cosx|在[kπ+
π,kπ+
π]递减,
根据复合函数的单调性得:
∴函数f(x)在(kπ+
,kπ+
π]递减,在[kπ+
π,kπ+
π]递增.
| π |
| 4 |
∴函数的定义域为{x|x≠kπ+
| π |
| 4 |
由sinx-cosx=
| 2 |
| π |
| 4 |
| 2 |
∴f(x)=log
| 1 |
| 2 |
| 1 |
| 2 |
∴函数f(x)的值域是[-
| 1 |
| 2 |
(2)因为f(x)定义域在数轴上对应的点不关于原点对称,故f(x)是非奇非偶函数,
f(x)=
| log | |sinx-cosx|
|
| log | |
|
| log | |sin(x-
|
| 1 |
| 2 |
∵有绝对值,∴T=
| 2π |
| 2 |
(3)∵函数y=|sinx-cosx|=
| 2 |
| π |
| 4 |
由kπ<x-
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3 |
| 4 |
∴函数y=|sinx-cosx|在(kπ+
| π |
| 4 |
| 3 |
| 4 |
由kπ+
| π |
| 2 |
| π |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
∴函数y=|sinx-cosx|在[kπ+
| 3 |
| 4 |
| 5 |
| 4 |
根据复合函数的单调性得:
∴函数f(x)在(kπ+
| π |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
点评:本题考查函数的性质:函数的定义域、值域、单调性、奇偶性、周期性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对任意非零实数a,b,若a?b的运算法则如图的框图所示,则4?(lg100)的值等于( )


A、
| ||
B、
| ||
C、
| ||
D、
|
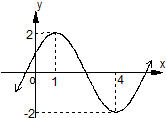 已知简谐运动f(x)=Asin(ωx+φ),(|φ|<
已知简谐运动f(x)=Asin(ωx+φ),(|φ|<| π |
| 2 |
则该简谐运动的最小正周期和初相φ分别为( )
A、T=6,φ=
| ||
B、T=6,φ=
| ||
C、T=6,φ=
| ||
D、T=6,φ=
|
