题目内容
函数y=f(x)是偶函数,当x≥0时,f(x)=x2-4x+3.
(1)求f(x);
(2)指出f(x)的单调区间;
(3)若当x∈[a,2a+1]时,f(x)的最大值为3,求a的取值集合.
(1)求f(x);
(2)指出f(x)的单调区间;
(3)若当x∈[a,2a+1]时,f(x)的最大值为3,求a的取值集合.
考点:函数奇偶性的性质,二次函数的性质
专题:函数的性质及应用
分析:(1)先设x<0,则-x>0,根据已知的函数解析式结合偶函数的定义式即可求出x<0时的解析式,则问题获解;
(2)根据二次函数的性质和图象即可得函数的单调区间;
(3)借助于函数图象即可得到区间[a,2a+1]要满足的关系式.
(2)根据二次函数的性质和图象即可得函数的单调区间;
(3)借助于函数图象即可得到区间[a,2a+1]要满足的关系式.
解答:
解:(1)函数y=f(x)是偶函数,当x≥0时,f(x)=x2-4x+3.
若x<0,可得-x>0,f(-x)=x2+4x+3,可得f(x)=f(-x)=x2+4x+3,
所以f(x)=
.
(2)由(1)得以f(x)=
.
画出f(x)的图象如下:
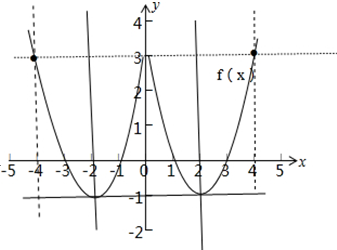
由图象可知:f(x)的单调增区间为:(2,+∞)和(-2,0);单调减区间为:(-∞,-2)和(0,2);
(3)因为当x∈[a,2a+1]时,f(x)的最大值为3,结合(2)的图象可以知道a与2a+1肯定在-4和4之间移动,
∴
解得-
≤a≤0,
若2a+1=4可得a=
,也满足题意;
∴a的取值集合:{a|-
≤a≤0或a=
}.
若x<0,可得-x>0,f(-x)=x2+4x+3,可得f(x)=f(-x)=x2+4x+3,
所以f(x)=
|
(2)由(1)得以f(x)=
|
画出f(x)的图象如下:

由图象可知:f(x)的单调增区间为:(2,+∞)和(-2,0);单调减区间为:(-∞,-2)和(0,2);
(3)因为当x∈[a,2a+1]时,f(x)的最大值为3,结合(2)的图象可以知道a与2a+1肯定在-4和4之间移动,
∴
|
| 1 |
| 2 |
若2a+1=4可得a=
| 3 |
| 2 |
∴a的取值集合:{a|-
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了利用函数的奇偶性确定函数的解析式、研究函数的图象进一步研究函数的性质.属于基础题,难度不大.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
抛物线y=4x2关于直线x-y=0对称的抛物线的准线方程是( )
| A、y=-1 | ||
B、y=-
| ||
| C、x=-1 | ||
D、x=-
|
在数列{an}中,a1=1,an+1=
(n∈N*),则a3的值为( )
| 2an |
| an+2 |
A、
| ||
B、
| ||
C、
| ||
D、
|