题目内容
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
考点:圆的标准方程
专题:直线与圆
分析:令m=cosθ,n=sinθ+1,由条件可得c≥-m-n 恒成立.求得-m-n=-
sin(θ+
)-1 的最大值,可得c的范围.
| 2 |
| π |
| 4 |
解答:
解:由题意可得,m2+(n-1)2=1,
令 m=cosθ,n=sinθ+1,
∵m+n+c≥0恒成立,∴c≥-m-n 恒成立.
∵-m-n=-cosθ-sinθ-1=-
sin(θ+
)-1 的最大值为
-1,
∴c≥
-1,
故选:D.
令 m=cosθ,n=sinθ+1,
∵m+n+c≥0恒成立,∴c≥-m-n 恒成立.
∵-m-n=-cosθ-sinθ-1=-
| 2 |
| π |
| 4 |
| 2 |
∴c≥
| 2 |
故选:D.
点评:本题主要考查圆的标准方程,三角函数的恒等变换,正弦函数的最值,属于中档题.

练习册系列答案
相关题目
设非零向量
,
,
,满足|
+
|=|
-
|,且|
|=|
|=|
+
+
|=1,则|
|的取值范围是( )
| x |
| y |
| z |
| x |
| y |
| x |
| y |
| x |
| y |
| x |
| y |
| z |
| ||||
|
|
| A、[0,2] | ||||||||
B、[1-
| ||||||||
C、[0,
| ||||||||
| D、[1,2] |
某几何体的三视图如图所示,则该几何体的体积为( )


| A、45π | B、54π |
| C、72π | D、90π |
“m=2”是“直线l1:mx+4y-6=0与直线l2:x+my-3=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知命题p:平行于同一直线的两个平面平行;命题q:垂直于同一平面的两条直线平行,那么( )
| A、“p或q”是假命题 |
| B、“p且q”是真命题 |
| C、“¬p或q”是假命题 |
| D、“¬p且q”是真命题 |
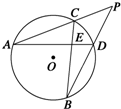 如图所示,⊙O的两条弦AD和CB相交于点E,AC和BD的延长线相交于点P,下面结论:
如图所示,⊙O的两条弦AD和CB相交于点E,AC和BD的延长线相交于点P,下面结论:①PA•PC=PD•PB;
②PC•CA=PB•BD;
③CE•CD=BE•BA;
④PA•CD=PD•AB.
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
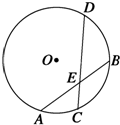 如图所示,已知⊙O的半径为5,两弦AB、CD相交于AB的中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )
如图所示,已知⊙O的半径为5,两弦AB、CD相交于AB的中点E,且AB=8,CE:ED=4:9,则圆心到弦CD的距离为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|