题目内容
“m=2”是“直线l1:mx+4y-6=0与直线l2:x+my-3=0平行”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据两条直线平行的条件,建立关于m的关系式,利用充分条件和必要条件的定义进行判断.
解答:
解:当m=2,;两直线方程分别为:2x+4y-6=0与直线x+2y-3=0此时两直线重合,充分性不成立.
若直线l1:mx+4y-6=0与直线l2:x+my-3=0平行,
则当m=0时,两直线方程分别为4y-6=0或x-3=0,此时两直线不平行,
当m≠0,若两直线平行,则
=
≠
,
即m2=4且m≠2,解得m=-2,即必要性不成立,
故“m=2”是“直线l1:mx+4y-6=0与直线l2:x+my-3=0平行”的既不充分也不必要条件,
故选:D.
若直线l1:mx+4y-6=0与直线l2:x+my-3=0平行,
则当m=0时,两直线方程分别为4y-6=0或x-3=0,此时两直线不平行,
当m≠0,若两直线平行,则
| m |
| 1 |
| 4 |
| m |
| -6 |
| -3 |
即m2=4且m≠2,解得m=-2,即必要性不成立,
故“m=2”是“直线l1:mx+4y-6=0与直线l2:x+my-3=0平行”的既不充分也不必要条件,
故选:D.
点评:本题在两条直线平行的情况下求参数m的值.着重考查了直线的方程与直线的位置关系等知识,属于基础题.在判断两条直线平行时,应该注意两条直线不能重合,否则会出现多解而致错.

练习册系列答案
相关题目
已知i是虚数单位,复数
=1-bi,其中a、b∈R,则|a+bi|等于( )
| 2-ai |
| i |
| A、-1+2i | ||
| B、1 | ||
C、
| ||
| D、5 |
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
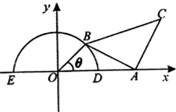 如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )
如图,半圆的圆心在直角坐标原点,点A,D,E的坐标分别为A(2,0),D(1,0),E(-1,0),且点B在半圆上自点D逆时针向点E运动,三角形ABC是等腰直角三形,∠BAC是直角,则四边形OACB的面积的最大值是( )A、
| ||||
B、2+2
| ||||
C、
| ||||
D、2+
|
i是虚数单位,复数
-(1-i)2=( )
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
在复平面内,复数z和(2-i)i表示的点关于虚轴对称,则复数z=( )
| A、1+2i | B、-1+2i |
| C、-1-2i | D、1-2i |
已知复数z=
,则|z|=( )
| 5 |
| 1+2i |
| A、1 | ||||
B、
| ||||
C、
| ||||
| D、5 |
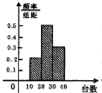
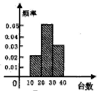
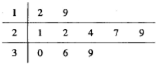 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )