题目内容
若x∈R,用[x]表示不超过x的最大整数,如[-1.5]=-2,[5.1]=5,设{x}=x-[x],则对函数f(x)={x},下列说法中正确的个数是( )
①定义域为R,值域为[0,1);
②它是以1为周期的周期函数;
③若方程f(x)=kx+k有三个不同的根,则实数k的取值范围是(-
,-
]∪[
,
);
④若n≤x1≤x2<n+1(n∈Z),则f(x1)≤f(x2).
①定义域为R,值域为[0,1);
②它是以1为周期的周期函数;
③若方程f(x)=kx+k有三个不同的根,则实数k的取值范围是(-
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
④若n≤x1≤x2<n+1(n∈Z),则f(x1)≤f(x2).
| A、1 | B、2 | C、3 | D、4 |
考点:函数的图象
专题:
分析:抓住n≤x<n+1时,f(x)=x-n这一特征进行求解.
解答:
解:①函数f(x)定义域为R,假设n≤x<n+1,则f(x)=x-n∈[0,1),即①正确;
②假设n≤x<n+1,n+1≤x<n+2(n∈Z),则f(x)=x-n,f(x+1)=x+1-n-1=x-n,即f(x)=f(x+1),②正确;
③方程f(x)=kx+k有三个不同的根,即函数f(x)的图象与直线y=kx+k有三个不同交点,结合图象可知,k的取值范围应为(-1,-
]∪[
,
),即③错误;
④若n≤x1≤x2<n+1(n∈Z),则f(x1)=x1-n,f(x2)=x2-n,故f(x1)≤f(x2),④正确.
故选:C.
②假设n≤x<n+1,n+1≤x<n+2(n∈Z),则f(x)=x-n,f(x+1)=x+1-n-1=x-n,即f(x)=f(x+1),②正确;
③方程f(x)=kx+k有三个不同的根,即函数f(x)的图象与直线y=kx+k有三个不同交点,结合图象可知,k的取值范围应为(-1,-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
④若n≤x1≤x2<n+1(n∈Z),则f(x1)=x1-n,f(x2)=x2-n,故f(x1)≤f(x2),④正确.
故选:C.
点评:本题在高斯函数的背景下考查了函数的图象与性质,有一定的难度.解题时,要牢牢抓住n≤x<n+1时,f(x)=x-n这一特征.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
执行如图所示的程序框图(算法流程图),则输出结果是( )


| A、0 | ||
B、
| ||
C、
| ||
D、
|
若当P(m,n)为圆x2+(y-1)2=1上任意一点时,不等式m+n+c≥0恒成立,则c的取值范围是( )
A、-1-
| ||||
B、
| ||||
C、c≤-
| ||||
D、c≥
|
cos240°=( )
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
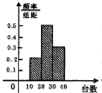
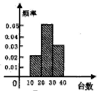
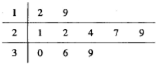 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )