题目内容
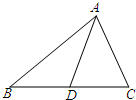如图，已知△ABC中，∠BAD=30°，∠CAD=45°，AB=3，AC=2，则| BD |
| DC |
考点：正弦定理
专题：计算题,解三角形
分析：过C作CE∥AB，与AD的延长线相交于E，则∠AEC=30°，在△AEC中，利用正弦定理，求出CE，再利用
=
，即可得出结论．
| BD |
| DC |
| AB |
| CE |
解答：
解：过C作CE∥AB，与AD的延长线相交于E，则∠AEC=30°．
在△AEC中，∵∠CAD=45°，∴
=
，
∴CE=2
，
∵CE∥AB，AB=3，
∴
=
=
=
．
故答案为：
．
解：过C作CE∥AB，与AD的延长线相交于E，则∠AEC=30°．在△AEC中，∵∠CAD=45°，∴
| 2 |
| sin30° |
| CE |
| sin45° |
∴CE=2
| 2 |
∵CE∥AB，AB=3，
∴
| BD |
| DC |
| AB |
| CE |
| 3 | ||
2
|
3
| ||
| 4 |
故答案为：
3
| ||
| 4 |
点评：本题考查正弦定理，考查平行线分线段成比例，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目