题目内容
容器A内装有6升质量分数为20%的盐水溶液，容器B内装有4升质量分数为5%的盐水溶液，先将A内的盐水倒1升进入B内，再将B内的盐水倒1升进入A内，称为一次操作；这样反复操作n次，A、B容器内的盐水的质量分数分别为an，bn，
（1）求a1、b1，并证明{an-bn}是等比数列；
（2）至少操作多少次，A、B两容器内的盐水浓度之差小于1%？（取lg2=0.3010，lg3=0.4771）；
（3）求an、bn的表达式．
（1）求a1、b1，并证明{an-bn}是等比数列；
（2）至少操作多少次，A、B两容器内的盐水浓度之差小于1%？（取lg2=0.3010，lg3=0.4771）；
（3）求an、bn的表达式．
考点：数列的应用
专题：应用题,点列、递归数列与数学归纳法
分析：（1）先根据条件求出b1=
(
+4×
)=
，a1=
(
+5×
)=
；bn+1=
，an+1=
（5an+bn+1）=
，即可证明{an-bn}是等比数列；
（2）由（1）知an-bn=
×(
)n-1，再结合盐水浓度之差小于1%，借助于对数的性质解不等式即可求出答案．
（3）先根据bn+1=
[bn+
×(
)n-1+4bn]，可得bn+1-bn=
×(
)n，利用叠加法，即可求出bn的通项以及an的表达式．
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 20 |
| 2 |
| 25 |
| 1 |
| 6 |
| 2 |
| 25 |
| 1 |
| 5 |
| 9 |
| 50 |
| an+4bn |
| 5 |
| 1 |
| 6 |
| 26an+4bn |
| 30 |
（2）由（1）知an-bn=
| 1 |
| 10 |
| 2 |
| 3 |
（3）先根据bn+1=
| 1 |
| 5 |
| 1 |
| 10 |
| 2 |
| 3 |
| 3 |
| 100 |
| 2 |
| 3 |
解答：
解：（1）由题意，b1=
(
+4×
)=
，a1=
(
+5×
)=
；
∵bn+1=
，an+1=
（5an+bn+1）=
，
∴an+1-bn+1=
（an-bn）
∴{an-bn}是等比数列；
（2）由（1）知an-bn=
×(
)n-1，
∴
×(
)n-1＜1%，
∴n-1＞
≈5.7
∴n≥7，故至少操作7次；
（3）∵bn+1=
[bn+
×(
)n-1+4bn]，
∴bn+1-bn=
×(
)n
∴bn=b1+（b2-b1）+（b3-b2）+…+（bn-bn-1）=
+
×[
+…+(
)n-1]=-
×(
)n+
，
∴an=bn+
×(
)n-1=
×(
)n+
．
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 20 |
| 2 |
| 25 |
| 1 |
| 6 |
| 2 |
| 25 |
| 1 |
| 5 |
| 9 |
| 50 |
∵bn+1=
| an+4bn |
| 5 |
| 1 |
| 6 |
| 26an+4bn |
| 30 |
∴an+1-bn+1=
| 2 |
| 3 |
∴{an-bn}是等比数列；
（2）由（1）知an-bn=
| 1 |
| 10 |
| 2 |
| 3 |
∴
| 1 |
| 10 |
| 2 |
| 3 |
∴n-1＞
| 1 |
| lg3-lg2 |
∴n≥7，故至少操作7次；
（3）∵bn+1=
| 1 |
| 5 |
| 1 |
| 10 |
| 2 |
| 3 |
∴bn+1-bn=
| 3 |
| 100 |
| 2 |
| 3 |
∴bn=b1+（b2-b1）+（b3-b2）+…+（bn-bn-1）=
| 2 |
| 25 |
| 3 |
| 100 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 100 |
| 2 |
| 3 |
| 7 |
| 50 |
∴an=bn+
| 1 |
| 10 |
| 2 |
| 3 |
| 3 |
| 50 |
| 2 |
| 3 |
| 7 |
| 50 |
点评：本题考查数列的性质和应用，根据题意找到两种容器内的盐水浓度的差bn-an的规律是关键．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知函数g（x）=ax3+bx2+cx+d（a≠0）的导函数为f（x），且a+2b+3c=0，f（0）•f（1）＞0，设x1，x2是方程f（x）=0的两根，则|x1-x2|的取值范围是（ ）
A、[0，
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
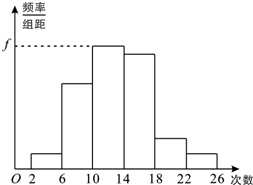为了解某校学生暑期参加体育锻炼的情况，对某班M名学生暑期参加体育锻炼的次数进行了统计，得到如下的频率分布表与直方图：