题目内容
若函数f(x)=(
)x,且f(2x+1)=2f(2x),则满足条件的实数x的值为 .
| 1 |
| 2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:直接解指数方程即可得到结论.
解答:
解:∵f(x)=(
)x,
∴由f(2x+1)=2f(2x),
得(
) 2x+1=2×(
)2x=(
)2x-1,
∴2x+1=2x-1,
即2x=-1,∴方程无解,
即满足条件的实数x的值不存在.
故答案为:不存在.
| 1 |
| 2 |
∴由f(2x+1)=2f(2x),
得(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴2x+1=2x-1,
即2x=-1,∴方程无解,
即满足条件的实数x的值不存在.
故答案为:不存在.
点评:本题主要考查指数幂的化简和求解,利用指数函数的性质是解决本题的关键,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=(1+i)(1-i)在复平面内对应的点的坐标为( )
| A、(1,0) |
| B、(0,2) |
| C、(0,1) |
| D、(2,0) |
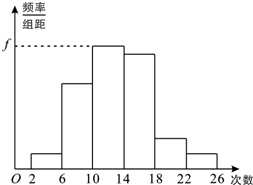 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图: