题目内容
当x∈(-2,-1)时,不等式x4+mx2+1<0恒成立,则实数m的取值范围是 .
考点:函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:令t=x2,由于x∈(-2,-1),则t∈(1,4),则不等式x4+mx2+1<0恒成立,即为f(t)=t2+mt+1<0在(1,4)恒成立,则有f(1)≤0且f(4)≤0,解得即可.
解答:
解:令t=x2,由于x∈(-2,-1),则t∈(1,4),
则不等式x4+mx2+1<0恒成立,即为t2+mt+1<0在(1,4)恒成立,
则由于抛物线f(t)=t2+mt+1,开口向上,则有f(1)≤0且f(4)≤0,
即为m+2≤0且17+4m≤0,即有m≤-2且m≤-
,
解得,m≤-
.
故答案为:(-∞,-
].
则不等式x4+mx2+1<0恒成立,即为t2+mt+1<0在(1,4)恒成立,
则由于抛物线f(t)=t2+mt+1,开口向上,则有f(1)≤0且f(4)≤0,
即为m+2≤0且17+4m≤0,即有m≤-2且m≤-
| 17 |
| 4 |
解得,m≤-
| 17 |
| 4 |
故答案为:(-∞,-
| 17 |
| 4 |
点评:本题考查可化为二次不等式的恒成立问题,考查二次函数的图象和性质,考查运算能力,属于中档题.

练习册系列答案
相关题目
过抛物线y2=2px(p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、QQ1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF,QF的长度分别是4,9,那么|PQ1|=( )
| A、12 | ||
| B、13 | ||
C、4
| ||
| D、15 |
当a>1时,在同一坐标系中,函数y=a-x与y=logax的图象为( )
A、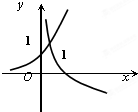 |
B、 |
C、 |
D、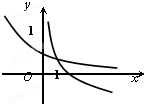 |
已知f(x)的图象如图所示,则下列数值按从小到大的排列顺序正确的是( )
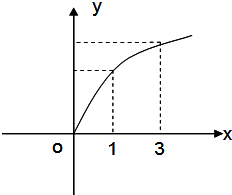

A、f′(1),f′(3),f(0),
| ||
B、f(0),f′(3),
| ||
C、
| ||
D、f(0),
|
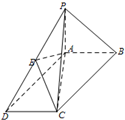 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.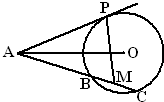 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,
如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,且与⊙O交于B、C两点,圆心O在∠PAC的内部,点M是BC的中点,