题目内容
已知
,则b+c的取值范围是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:以bc分别为xy轴作出不等式所对应的可行域,变形目标函数z=b+c可得c=-b+z,平移直线c=-b可知当直线经过点A时,目标函数取最大值,联立方程组,解之可得A的坐标,代值计算可得范围.
解答:
解:以bc分别为xy轴作出不等式所对应的可行域(如图阴影),
变形目标函数z=b+c可得c=-b+z,
平移直线c=-b可知当直线经过点A时,目标函数取最大值,
联立
可解得
,即A(-
,-6),
∴z=b+c的最大值为-
,
∴b+c的取值范围为(-∞,-
]
故答案为:(-∞,-
]
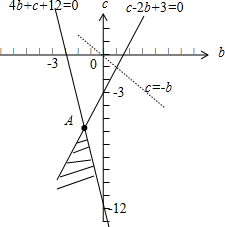
变形目标函数z=b+c可得c=-b+z,
平移直线c=-b可知当直线经过点A时,目标函数取最大值,
联立
|
|
| 3 |
| 2 |
∴z=b+c的最大值为-
| 15 |
| 2 |
∴b+c的取值范围为(-∞,-
| 15 |
| 2 |
故答案为:(-∞,-
| 15 |
| 2 |
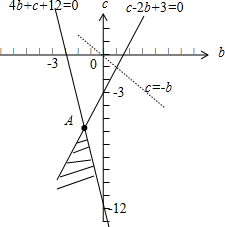
点评:本题考查简单选项规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
相关题目