题目内容
过抛物线y2=2px（p＞0）的焦点F作一直线l与抛物线交于P、Q两点，作PP1、QQ1垂直于抛物线的准线，垂足分别是P1、Q1，已知线段PF，QF的长度分别是4，9，那么|PQ1|=（ ）
| A、12 | ||
| B、13 | ||
C、4
| ||
| D、15 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：如图所示，过点P作PM⊥QQ1，垂足为M．可得四边形PMQ1P1为矩形，PM=P1Q1．利用抛物线的定义可得|PF|=|PP1|=4，|FQ|=|QQ1|=9，得到|QM|=9-4．在Rt△PQM中，利用勾股定理先求出|PM|=
，即可求出|PQ1|的值．
| |PQ|2-|QM|2 |
解答：
解：如图所示，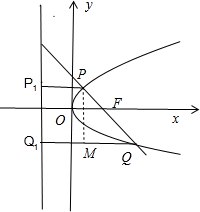
过点P作PM⊥QQ1，垂足为M．
则四边形PMQ1P1为矩形，∴PM=P1Q1．
∵|PF|=|PP1|=4，|FQ|=|QQ1|=9，∴|QM|=9-4=5．
在Rt△PQM中，|PM|=
=
=12．
∴|P1Q1|=12，∴|PQ1|=
=4
，
故选：C．
过点P作PM⊥QQ1，垂足为M．则四边形PMQ1P1为矩形，∴PM=P1Q1．
∵|PF|=|PP1|=4，|FQ|=|QQ1|=9，∴|QM|=9-4=5．
在Rt△PQM中，|PM|=
| |PQ|2-|QM|2 |
| 132-52 |
∴|P1Q1|=12，∴|PQ1|=
| |PM|2+|P1Q1|2 |
| 10 |
故选：C．
点评：本题考查了抛物线的定义、矩形的性质、勾股定理，属于基础题．
练习册系列答案
相关题目
函数f（x）=ax+b的图象如图所示，其中a，b为常数，则下列结论正确的是（ ）
| A、a＞1，b＜0 |
| B、a＞1，b＞0 |
| C、0＜a＜1，b＞0 |
| D、0＜a＜1，b＜0 |
直线2x+y+1=0与圆（x+1）2+（y-1）2=1的位置关系是（ ）
| A、相交 | B、相切 | C、相离 | D、不确定 |