题目内容
6.若函数f(x)=2sinx+acosx,且已知函数f(x)+f′(x)为偶函数,则实数a的值为2.分析 求出f(x)+f′(x)的解析式,利用函数奇偶性的性质进行判断.
解答 解:f′(x)=2cosx-asinx,
f(x)+f′(x)=(2-a)sinx+(a+2)cosx.
∵f(x)+f′(x)为偶函数,
∴2-a=0,即a=2.
故答案为:2.
点评 本题考查了函数奇偶性的性质,三角函数的导数运算,三角函数的图象与性质,属于中档题.

练习册系列答案
相关题目
17.函数y=3sinx-5cosx的最大值是( )
| A. | -4 | B. | -2 | C. | 4 | D. | $\sqrt{34}$ |
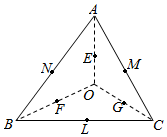 平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
 ,
, ;
; 的解集;
的解集; ,
, ,求
,求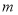 的取值范围.
的取值范围.