题目内容
11.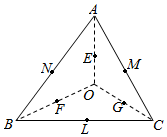 平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.
平面内有一个△ABC和一点O(如图),线段OA,OB,OC的中点分别为E,F,G,BC,CA,AB的中点分别为L,M,N,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$.(1)试用$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示向量$\overrightarrow{EL}$,$\overrightarrow{FM}$,$\overrightarrow{GN}$;
(2)证明:线段EL,FM,GN交于一点且互相平分.
分析 (1)根据向量的加法、数乘的几何意义,以及向量加法的平行四边形法则,并进行向量的数乘运算便可得到$\overrightarrow{EL}=-\frac{1}{2}\overrightarrow{a}+\frac{1}{2}(\overrightarrow{b}+\overrightarrow{c})=\frac{1}{2}(-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$,从而同理可以用$\overrightarrow{a},\overrightarrow{b},\overrightarrow{c}$分别表示出$\overrightarrow{FM},\overrightarrow{GN}$;
(2)可连接EN,NL,LG,GE,根据三角形中位线的性质及平行四边形的定义便可得到四边形NLGE为平行四边形,从而对角线EL,GN交于一点且互相平分,而同理可证明EL,FM相交于一点且互相平分,从而便得出线段EL,FM,GN交于一点且互相平分.
解答 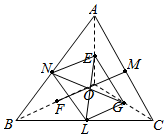 解:(1)$\overrightarrow{EL}=\overrightarrow{EO}+\overrightarrow{OL}=-\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$=$\frac{1}{2}(-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$;
解:(1)$\overrightarrow{EL}=\overrightarrow{EO}+\overrightarrow{OL}=-\frac{1}{2}\overrightarrow{OA}+\frac{1}{2}(\overrightarrow{OB}+\overrightarrow{OC})$=$\frac{1}{2}(-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})$;
同理,$\overrightarrow{FM}=\frac{1}{2}(-\overrightarrow{b}+\overrightarrow{a}+\overrightarrow{c})$,$\overrightarrow{GN}=\frac{1}{2}(-\overrightarrow{c}+\overrightarrow{a}+\overrightarrow{b})$;
(2)证明:如图,连接EN,NL,LG,GE,根据条件,则:
NE∥BO,且$NE=\frac{1}{2}BO$,LG∥BO,且$LG=\frac{1}{2}BO$;
∴NE∥LG,且NE=LG;
∴四边形NLGE为平行四边形;
∴线段El,GN交于一点且互相平分;
同理,线段EL,FM交于一点且互相平分;
∴线段EL,FM,GN交于一点且互相平分.
点评 考查向量加法、数乘的几何意义,向量加法的平行四边形法则,以及向量的数乘运算,三角形中位线的性质,平行四边形的概念,平行四边形的对角线相交于一点且互相平分.

| A. | [-$\frac{2}{3}$,2] | B. | (-∞,-$\frac{2}{3}$)∪[2,+∞) | C. | (-$\frac{2}{3}$,2] | D. | (-∞,-$\frac{2}{3}$]∪[2,+∞) |
 执行如图所示程序框图,若将输出的数组(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),则程序结束时,最后一次输出的数组(x,y)是( )
执行如图所示程序框图,若将输出的数组(x,y)依次记为(x1,y1),(x2,y2),…,(xn,yn),则程序结束时,最后一次输出的数组(x,y)是( )| A. | (1007,-2012) | B. | (1009,-2016) | C. | (1008,-2014) | D. | (1010,-2018) |
 如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC.
如图已知三棱锥P-ABC,PA⊥平面ABC,AB=AC=PA=2,∠BAC=90°,D,E分别为AB,PC的中点,BF=2FC. 中,
中, ,
, ,平面
,平面 平面
平面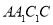 ,
,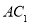 与
与 相交于点
相交于点 .
.
 ;
; 的余弦值.
的余弦值.