题目内容
用数学归纳法证明:
≤n+1(n∈N*).
| n2+n |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:本题考查的知识点是数学归纳法,由数学归纳法的步骤,我们先判断n=1时成立,然后假设当n=k时成立,只要能证明出当n=k+1时,结论成立,立即可得到所有的正整数n都成立.
解答:
证明:①n=1时,左边=
,右边=2,
<2成立;
②设n=k时,结论成立,即
≤k+1,即k+1≥0
则n=k+1时,左边=
≤
<k+2,
∴n=k+1时,成立.
由①②可知,
≤n+1(n∈N*).
| 2 |
| 2 |
②设n=k时,结论成立,即
| k2+k |
则n=k+1时,左边=
| (k+1)2+(k+1) |
| (k+1)2+2k+2 |
∴n=k+1时,成立.
由①②可知,
| n2+n |
点评:数学归纳法的步骤:①证明n=1时A式成立②然后假设当n=k时,A式成立③证明当n=k+1时,A式也成立④下绪论:A式对所有的正整数n都成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知抛物线x2=4y上有一点长为6的弦AB所在直线倾斜角为45°,则AB中点到x轴的距离为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知a>0,b>0,且4a-b≥0,若函数f(x)=
ax3+x2+bx无极值,则
的取值范围为( )
| 1 |
| 3 |
| b-2 |
| a+1 |
A、[2
| ||
B、[2
| ||
C、[-2
| ||
D、[-2
|
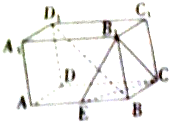 如图所示,长方体ABCD-A1B1C1D1的侧面BCC1B1是正方形,E是AB的中点,AB=
如图所示,长方体ABCD-A1B1C1D1的侧面BCC1B1是正方形,E是AB的中点,AB=