题目内容
已知P为等腰△ABC内一点,AB=BC,∠BPC=108°.D为AC的中点,BD与PC交于点E,如果P为△ABE的内心,则∠PAC的度数是 .
考点:正弦定理
专题:解三角形
分析:先画图,由对顶角,三角形全等可得∠PEA=∠PEB=∠CED=∠AED=60°,即可求∠PCA,∠PBE,∠ABD,∠BAD,∠PAE的值,由∠PAC=∠PAE+∠CAE即可得解.
解答:
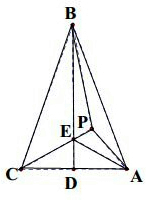 解:由题意可得:∠PEA=∠PEB=∠CED=∠AED,
解:由题意可得:∠PEA=∠PEB=∠CED=∠AED,
而∠PEA+∠PEB+AED=180°,
所以∠PEA=∠PEB=∠CED=∠AED=60°,
所以可得∠PCA=30°,
又∠BPC=108°,所以∠PBE=12°,从而∠ABD=24°,
所以∠BAD=90°-24°=66°,
所以∠PAE=
(∠BAD-∠CAE)=
(66°-30°)=18°,
所以∠PAC=∠PAE+∠CAE=18°+30°=48°.
故答案为:48°.
 解:由题意可得:∠PEA=∠PEB=∠CED=∠AED,
解:由题意可得:∠PEA=∠PEB=∠CED=∠AED,而∠PEA+∠PEB+AED=180°,
所以∠PEA=∠PEB=∠CED=∠AED=60°,
所以可得∠PCA=30°,
又∠BPC=108°,所以∠PBE=12°,从而∠ABD=24°,
所以∠BAD=90°-24°=66°,
所以∠PAE=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠PAC=∠PAE+∠CAE=18°+30°=48°.
故答案为:48°.
点评:本题主要考查了等腰三角形的性质,三角形的全等,三角形内心,三角形内角和等知识的应用,考查了分析问题解决问题的能力,考查了转化思想,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
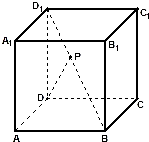 如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
如图,点P在正方体ABCD-A1B1C1D1 的对角线BD1上,且cos∠PDA=
| ||
| 4 |
| A、75° | B、60° |
| C、45° | D、30° |
函数f(x)=cos
(
sin
+cos
)的在下列哪个区间上单调递增( )
| x |
| 2 |
| 3 |
| x |
| 2 |
| x |
| 2 |
A、(
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|