题目内容
对于函数f(x),我们把使得f(x)=x成立的x称为函数f(x)的“不动点”;把使得f(f(x))=x成立的x称为函数f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”构成的集合分别记为A和B,即A={x|f(x)=x},B={x|f(f(x))=x}.
(1)求证:A⊆B;
(2)若f(x)=2x-1,求集合B;
(3)若f(x)=x2-a,且A=B≠∅,求实数a的取值范围.
(1)求证:A⊆B;
(2)若f(x)=2x-1,求集合B;
(3)若f(x)=x2-a,且A=B≠∅,求实数a的取值范围.
考点:二次函数的性质,函数的值
专题:函数的性质及应用
分析:(1)分类求解若A=∅,则A⊆B显然成立; 若A≠∅,
(2)得出f(f(t))=2(2x-1)-1=4x-3=x,求解即可.
(3)分类①△<0,a<
时,C=∅⊆A成立②△=0,A=
时,C={-
},A={-
,
},C⊆A成立③△>0,总结即可.
(2)得出f(f(t))=2(2x-1)-1=4x-3=x,求解即可.
(3)分类①△<0,a<
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)若A=∅,则A⊆B显然成立;
若A≠∅,
设t∈A,则f(t)=t,f(f(t))=f(t)=t
∴t∈B,
故A⊆B
(2)∵f(x)=2x-1,
∴f(f(t))=2(2x-1)-1=4x-3=x,
∴x=1
∴B={1}
(3)∵A≠∅有实根,∴a≥-
方程f(f(t))=(x2-a)2-a=x,可化为(x2-x-a)(x2+x-a+1)=0
设方程x2+x-a+1=0的解集为C,方程f(f(x))=x的解集B═A∪C
∵A=B,∴C⊆A
方程x2+x-a+1=0的判别式△=4a-3
①△<0,a<
时,C=∅⊆A成立
②△=0,A=
时,C={-
},A={-
,
},C⊆A成立
③△>0,a>
时,不合题意
由①②③得a≤
综上所述 a∈[-
,
]
若A≠∅,
设t∈A,则f(t)=t,f(f(t))=f(t)=t
∴t∈B,
故A⊆B
(2)∵f(x)=2x-1,
∴f(f(t))=2(2x-1)-1=4x-3=x,
∴x=1
∴B={1}
(3)∵A≠∅有实根,∴a≥-
| 1 |
| 4 |
方程f(f(t))=(x2-a)2-a=x,可化为(x2-x-a)(x2+x-a+1)=0
设方程x2+x-a+1=0的解集为C,方程f(f(x))=x的解集B═A∪C
∵A=B,∴C⊆A
方程x2+x-a+1=0的判别式△=4a-3
①△<0,a<
| 3 |
| 4 |
②△=0,A=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
③△>0,a>
| 3 |
| 4 |
由①②③得a≤
| 3 |
| 4 |
综上所述 a∈[-
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题考查了集合,函数的性质,方程等问题,属于中档题,计算较麻烦,分类清晰,讨论详细.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
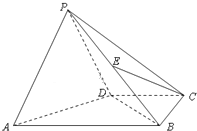 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,∠ABC=∠BCD=90°,PA=PD=DC=CB=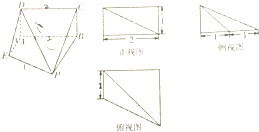 已知一个空间几何体的直观图和三视图(尺寸如图所示)
已知一个空间几何体的直观图和三视图(尺寸如图所示)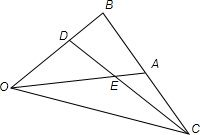 如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设
如图,已知△OAB中,点C是点B关于A的对称点,点D是线段OB的一个靠近B的三等分点,DC和OA交于E,设