题目内容
5.f(x)=$\frac{x}{{x}^{2}+1}$(x≤0)的值域为[-$\frac{1}{2}$,0].分析 求导,解出f′(x)=0,判断x=-1为函数的极小值点,故可求出函数的值域.
解答 解:f(x)=$\frac{x}{{x}^{2}+1}$(x≤0),
f′(x)=$\frac{{x}^{2}+1-x•2x}{({x}^{2}+1)^{2}}$=$\frac{1-{x}^{2}}{({x}^{2}+1)^{2}}$,(x≤0),
f′(x)=0,解得x=-1,
x<-1,f′(x)<0,f(x)单调递减,
-1<x≤0,f′>(x)0,f(x)单调递增,
当x=-1取极小值,为-$\frac{1}{2}$,也为最小值,
∴f(x)=$\frac{x}{{x}^{2}+1}$(x≤0)的值域为[-$\frac{1}{2}$,0],
故答案为:[-$\frac{1}{2}$,0].
点评 本题考查利用导数求函数的值域,要熟练掌握函数的求导法则,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.平面直角坐标系xOy中,双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线C2:y2=2px(p>0)交于点O,A,B,若△OAB的重心为C2的焦点,则C1的渐近线方程为( )
| A. | y=±$\frac{\sqrt{6}}{4}$x | B. | y=±$\frac{2\sqrt{6}}{3}$x | C. | y=±2$\sqrt{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.若命题“?x∈[0,$\frac{π}{2}$],不等式exsinx≥kx”是真命题,则实数k的取值范围是( )
| A. | (-∞,1] | B. | (-∞,e${\;}^{\frac{π}{2}}$] | C. | (1,e${\;}^{\frac{π}{2}}$) | D. | [e${\;}^{\frac{π}{2}}$,+∞) |
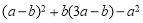 ,其中
,其中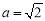 ,
,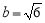 .
.