题目内容
9.已知数列{an}满足an+3an+1=0,a4=-$\frac{4}{27}$,则数列{an}的前10项和S10=3(1-$\frac{1}{{3}^{10}}$).分析 化简可判断数列{an}是以4为首项,-$\frac{1}{3}$为公比的等比数列,从而求和.
解答 解:∵an+3an+1=0,∴an+1=-$\frac{1}{3}$an,
又∵a4=-$\frac{4}{27}$≠0,
∴数列{an}是以-$\frac{1}{3}$为公比的等比数列,
∴an=a4•(-$\frac{1}{3}$)n-4=4•(-$\frac{1}{3}$)n-1,
∴数列{an}是以4为首项,-$\frac{1}{3}$为公比的等比数列,
∴S10=$\frac{4(1-(-\frac{1}{3})^{10})}{1+\frac{1}{3}}$=3(1-$\frac{1}{{3}^{10}}$),
故答案为:3(1-$\frac{1}{{3}^{10}}$).
点评 本题考查了等比数列的性质的判断与应用.

练习册系列答案
相关题目
2.M为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,A、F分别为双曲线的左顶点和右焦点,且△MAF为等边三角形,则双曲线C的离心率为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | 4 | D. | 6 |
2.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(b-a)sinA=(b-c)(sinB+sinC),则角C等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
13.函数f(x)=$\frac{1}{3}$x3-ax2-3a2x-4在(3,+∞)上是增函数,则实数a的取值范围是( )
| A. | a≥0 | B. | a≥1 | C. | a≤-3或a≥1 | D. | -3≤a≤1 |
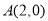 的直线
的直线 与
与 轴交于点
轴交于点 ,
,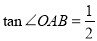 ,直线
,直线 位于
位于 轴左侧,且到
轴左侧,且到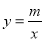 的图象经过点
的图象经过点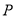 ,求
,求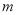 的值.
的值.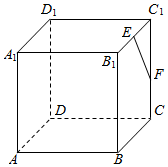 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求: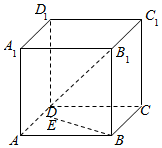 如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].
如图,已知正方体ABCD-A1B1C1D1中,E是平面ABCD上一动点,则直线BE与直线B1D所成角的余弦值的取值范围是[0,$\frac{\sqrt{6}}{3}$].