题目内容
已知一个袋子里有形状一样仅颜色不同的6个小球,其中白球2个,黑球4个.现从中随机取球,每次只取一球.
(1)若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
(2)若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.
(1)若每次取球后都放回袋中,求事件“连续取球四次,至少取得两次白球”的概率;
(2)若每次取球后都不放回袋中,且规定取完所有白球或取球次数达到五次就终止游戏,记游戏结束时一共取球X次,求随机变量X的分布列与期望.
考点:离散型随机变量的期望与方差,列举法计算基本事件数及事件发生的概率,离散型随机变量及其分布列
专题:概率与统计
分析:(1)记事件Ai表示“第i次取到白球”(i∈N*),事件B表示“连续取球四次,至少取得两次白球”,则:
=
+A1
+
A2
+
A3
+
A4,由此利用对立事件概率计算公式能求出事件“连续取球四次,至少取得两次白球”的概率.
(2)随机变量X的取值分别为2,3,4,5,分别求出相应的概率,由此能求出随机变量X的分布列与期望.
. |
| B |
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
(2)随机变量X的取值分别为2,3,4,5,分别求出相应的概率,由此能求出随机变量X的分布列与期望.
解答:
解:(1)记事件Ai表示“第i次取到白球”(i∈N*),
事件B表示“连续取球四次,至少取得两次白球”,
则:
=
+A1
+
A2
+
A3
+
A4.…(2分)
∴P(
)=P(
)+P(A1
)+P(
A2
)+P(
A3
)+P(
A4)
=(
)4+
×(
)3×4=
,…(4分)
∴P(B)=1-P(
)=1-
=
.…(5分)
(2)随机变量X的取值分别为2,3,4,5 …(6分)
P(X=2)=
=
,
P(X=3)=
×
=
,
P(X=4)=
×
=
,
P(X=5)=1-
-
-
=
,…(10分)
∴随机变量X的分布列为:
…(11分)
∴随机变量X的期望为:EX=2×
+3×
+4×
+5×
=
.…(12分)
事件B表示“连续取球四次,至少取得两次白球”,
则:
. |
| B |
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
∴P(
. |
| B |
. |
| A1 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A2 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A3 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A4 |
. |
| A1 |
. |
| A2 |
. |
| A3 |
=(
| 4 |
| 6 |
| 2 |
| 6 |
| 4 |
| 6 |
| 16 |
| 27 |
∴P(B)=1-P(
. |
| B |
| 16 |
| 27 |
| 11 |
| 27 |
(2)随机变量X的取值分别为2,3,4,5 …(6分)
P(X=2)=
| ||
|
| 1 |
| 15 |
P(X=3)=
| ||||
|
| 1 |
| 4 |
| 2 |
| 15 |
P(X=4)=
| ||||
|
| 1 |
| 3 |
| 1 |
| 5 |
P(X=5)=1-
| 1 |
| 15 |
| 2 |
| 15 |
| 1 |
| 5 |
| 3 |
| 5 |
∴随机变量X的分布列为:
| X | 2 | 3 | 4 | 5 | ||||||||
| P |
|
|
|
|
∴随机变量X的期望为:EX=2×
| 1 |
| 15 |
| 2 |
| 15 |
| 1 |
| 5 |
| 3 |
| 5 |
| 13 |
| 3 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法及应用,是中档题.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知抛物线的方程为y2=2x,则其焦点坐标为( )
A、(0,
| ||
B、(
| ||
C、(±
| ||
D、(0,-
|
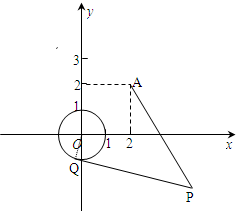 如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.
如图,已知⊙O:x2+y2=1和定点A(2,2),由⊙O外一点P(a,b)向⊙O引切线PQ,Q为切点,且满足|PQ|=|PA|.