题目内容
14．用秦九韶算法计算函数f（x）=2x5-3x3+2x2+x-3的值，若x=2，则V3的值是12．分析 先将函数的解析式分解为f（x）=（（（（2x+0）x-3）x+2）x+1）x-3的形式，进而根据秦九韶算法逐步代入即可得到答案．
解答 解：∵f（x）=2x5-3x3+2x2+x-3=（（（（2x+0）x-3）x+2）x+1）x-3
当x=2时，
v0=2
v1=4
v2=5
v3=12
故答案为12．
点评 本题考查的知识点秦九韶算法，熟练掌握秦九韶算法的方法和步骤是解答的关键．
练习册系列答案
相关题目
4．已知{an}为等差数列，若a1+a2+a3=$\frac{π}{2}$，a7+a8+a9=π，则cosa5的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | -$\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}$ |
2．△ABC中，已知a=7，b=14，A=30°，则△ABC有（ ）
| A． | 一解 | B． | 二解 | C． | 无解 | D． | 一解或二解 |
9．已知$|{\overrightarrow a}|=6\sqrt{3}，|{\overrightarrow b}|=\frac{1}{3}$，且$\overrightarrow a•\overrightarrow b=-3$，则$\overrightarrow a$与$\overrightarrow b$的夹角为（ ）
| A． | $\frac{π}{2}$ | B． | $\frac{π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{6}$ |
19．
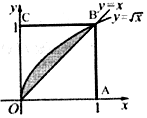向如图所示的正方形OABC内任意投一点，该点恰好落在图中阴影部分的概率为（ ）
向如图所示的正方形OABC内任意投一点，该点恰好落在图中阴影部分的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
3．复数$\frac{5i}{1+2i}$的虚部是（ ）
| A． | i | B． | -i | C． | 1 | D． | -1 |