题目内容
9.定义min{a,b}=$\left\{\begin{array}{l}{a,(a≤b)}\\{b,(a>b)}\end{array}\right.$,若函数f(x)=min{sin(2x+$\frac{π}{6}$),cos2x},且f(x)在区间[s,t]上的值域为[-1,$\frac{1}{2}$],则区间[s.t]长度的最大值为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{5π}{6}$ | D. | π |
分析 作出函数的图象,利用特殊角的三角函数值,即可得出结论.
解答  解:在同一坐标系中,作出函数f(x)=min{sin(2x+$\frac{π}{6}$),cos2x}的图象,
解:在同一坐标系中,作出函数f(x)=min{sin(2x+$\frac{π}{6}$),cos2x}的图象,
由cos2x=$\frac{1}{2}$,x取$\frac{π}{6}$,
sin(2x+$\frac{π}{6}$)=-1,
x取$\frac{2}{3}$π,
$\frac{2}{3}$π-$\frac{π}{6}$=$\frac{π}{2}$,
即f(x)在区间[s,t]上的值域为[-1,$\frac{1}{2}$],则区间[s,t]长度的最大值为$\frac{π}{2}$,
故选B.
点评 本题考查三角函数的图象,考查函数的最值,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
20.下列函数中,在(0,$\frac{π}{2}$)上是增函数的偶函数是( )
| A. | y=|sinx| | B. | y=|sin2x| | C. | y=|cosx| | D. | y=tanx |
4.已知{an}为等差数列,若a1+a2+a3=$\frac{π}{2}$,a7+a8+a9=π,则cosa5的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
14.表面积为20π的球面上有四点S、A、B、C,且△ABC是边长为2$\sqrt{3}$的等边三角形,若平面SAB⊥平面ABC,则三棱锥S-ABC体积的最大值是( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
1.已知等比数列{an}中,a2+a5=18,a3•a4=32,若an=128,则n=( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
19.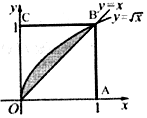 向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
 向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )
向如图所示的正方形OABC内任意投一点,该点恰好落在图中阴影部分的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
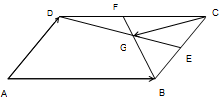 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量