题目内容
已知数列{an}中,a1=3,an+1=2an-1.
(1)求证:数列{an-1}是等比数列;
(2)设
,求证:数列{bn}的前n项和Sn<
.
(1)求证:数列{an-1}是等比数列;
(2)设
|
| 1 |
| 3 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据等比数列的定义,利用构造法即可证明数列{an-1}是等比数列;
(2)求出数列{bn}的通项公式,利用裂项法即可求出数列{bn}的前n项和Sn,即可证明不等式.
(2)求出数列{bn}的通项公式,利用裂项法即可求出数列{bn}的前n项和Sn,即可证明不等式.
解答:
解:(1)∵a1=3,an+1=2an-1,
∴an+1-1=2an-2=2(an-1),
即
=2,故数列{an-1}是等比数列.
(2)由(1)知数列{an-1}是等比数列,首项为a1-1=3-1=2,公比q=2,
则an-1=2•2n-1=2n,则an=1+2n,
则
=
=
=
-
,
则数列{bn}的前n项和Sn=
-
+
-
+…+
-
=
-
<
,
即Sn<
成立.
∴an+1-1=2an-2=2(an-1),
即
| an+1-1 |
| an-1 |
(2)由(1)知数列{an-1}是等比数列,首项为a1-1=3-1=2,公比q=2,
则an-1=2•2n-1=2n,则an=1+2n,
则
|
| 2n |
| (1+2n)(1+2n+1) |
| 1+2n+1-(1+2n) |
| (1+2n)(1+2n+1) |
| 1 |
| 1+2n |
| 1 |
| 1+2n+1 |
则数列{bn}的前n项和Sn=
| 1 |
| 1+2 |
| 1 |
| 1+22 |
| 1 |
| 1+22 |
| 1 |
| 1+23 |
| 1 |
| 1+2n |
| 1 |
| 1+2n+1 |
| 1 |
| 3 |
| 1 |
| 1+2n+1 |
| 1 |
| 3 |
即Sn<
| 1 |
| 3 |
点评:本题主要考查等比数列的证明,以及数列求和,利用裂项法是解决本题的关键.要求熟练掌握裂项技巧.

练习册系列答案
相关题目
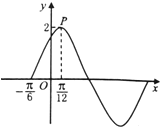 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,