题目内容
一个多面体的直观图、正(主)视图、侧(左)视图、俯视图如图,M、N分别为A1B、B1C1的中点.

下列结论中正确的是 .(填上所有正确项的序号)
①线MN与A1C 相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为V N-A1BC=
a3.

下列结论中正确的是
①线MN与A1C 相交;②MN⊥BC;③MN∥平面ACC1A1;④三棱锥N-A1BC的体积为V N-A1BC=
| 1 |
| 6 |
考点:简单空间图形的三视图,命题的真假判断与应用,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:取A1B1的中点D,连结DM、DN.根据中位线定理,线面平行的判定定理和面面平行的判断定理,可得平面DMN∥平面A1AC1C,可判断①,③;由三视图可得A1C1⊥平面BCC1B1,即DN⊥平面BCC1B1,即DN⊥BC,进而由线面垂直的判定定理得到BC⊥平面DMN,再由线面垂直的性质,可判断②;利用等积法,求出棱锥的体积,可判断④.
解答:
解:取A1B1的中点D,连结DM、DN.
由于M、N分别是所在棱的中点,
所以可得DN∥A1C1,DN?平面A1AC1C,A1C1?平面A1AC1C,所以DN∥平面A1AC1C.
同理可证DM∥平面A1AC1C.
又∵DM∩DN=D,
所以平面DMN∥平面A1AC1C,
所以直线MN与A1C 相交不成立,①错误;
由三视图可得A1C1⊥平面BCC1B1.
所以DN⊥平面BCC1B1,
所以DN⊥BC,
又易知DM⊥BC,
所以BC⊥平面DMN,
所以BC⊥MN,②正确;
由①中,平面DMN∥平面A1AC1C,
可得:③正确;
因为V N-A1BC=VA1-NBC=
(
a2)a=
a3,所以④正确.
综上,②③④正确.
故答案为:②③④
由于M、N分别是所在棱的中点,
所以可得DN∥A1C1,DN?平面A1AC1C,A1C1?平面A1AC1C,所以DN∥平面A1AC1C.
同理可证DM∥平面A1AC1C.
又∵DM∩DN=D,
所以平面DMN∥平面A1AC1C,
所以直线MN与A1C 相交不成立,①错误;
由三视图可得A1C1⊥平面BCC1B1.
所以DN⊥平面BCC1B1,
所以DN⊥BC,
又易知DM⊥BC,
所以BC⊥平面DMN,
所以BC⊥MN,②正确;
由①中,平面DMN∥平面A1AC1C,
可得:③正确;
因为V N-A1BC=VA1-NBC=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
综上,②③④正确.
故答案为:②③④
点评:本题以三视图为载体,考查了空间线面关系的判定与证明,棱锥的体积,命题的真假判断,综合性强,难度中档.

练习册系列答案
相关题目
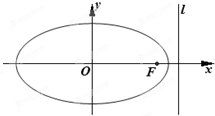 椭圆C的右焦点为F,右准线为l,离心率为
椭圆C的右焦点为F,右准线为l,离心率为