题目内容

在四面体ABCD中，AB=CD=3，AC=BD=AD=BC=4
2
，则该四面体外接球体积为
 
．
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：分别取AB，CD的中点E，F，连接相应的线段，由条件可知，球心G在EF上，可以证明G为EF中点，求出球的半径，然后求出球的表面积．
解答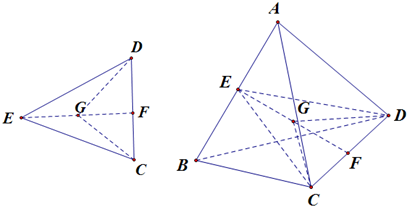： 解：分别取AB，CD的中点E，F，
连接相应的线段，由条件可知，EF是AB与CG的公垂线，球心G在EF上，可以证明G为EF中点，（△AGB≌△CGD）
DE=
32-
9
4
=
119
2

DF=
3
2
，
∴EF=
119
4
-
9
4
=
110
2
，
∴GF=
110
4
，
∴球半径DG=
110
16
+
9
4
=
146
4
，
∴四面体外接球体积为
4
3
π（
146
4
）3=
73
24
146
，
故答案为：
73
24
146
．
点评：本题考查球的内接几何体，球的体积的求法，考查计算能力．
练习册系列答案
相关题目
已知数列{an}中，a1=3，an+1=2an-1．
（1）求证：数列{an-1}是等比数列；
（2）设
bn=
2n
anan+1
，求证：数列{bn}的前n项和Sn＜
1
3
．
已知某几何体的三视图如图所示，则该几何体的体积等于
 
．
运行如图所示框图的相应程序，若输入a，b的值分别为
3
2
和
2
3
，则输出M的值是
 
．
给出下列四个命题：
（1）“cosα=-
3
2
”是“α=2kπ+
5π
6
，k∈Z”的必要不充分条件；
（2）终边在y轴上的角的集合是{a|a=
kπ
2
，k∈Z}．
（3）函数y=sin（2x-
π
3
）的一个单调增区间是[-
π
12
，
5π
12
]；
（4）设f（x）=sin（ωx+φ），其中ω＞0，则f（x）是偶函数的充要条件是f′（0）=0；
（5）为得到函数y=cos（2x+
π
3
）的图象，只需将函数y=sin2x的图象向左平移
5π
12
个长度单位．
其中真命题的序号是
 
（把所有真命题的序号都填上）．
某地高考规定每一考场安排24名考生，编成六行四列．若来自同一学校的甲、乙两名学生同时排在“××考点××考场”，那么他们两人前后左右均不相邻的不同的坐法总数有
 
 种．
若不等式|x-b|＜1的解集中的整数有且仅有1，则b的集合是
 
．
在△ABC中，设
BC
=（2-k，3），
AC
=（2，4）且|
AB
|≤4，k∈Z，则△ABC为直角三角形的概率为
 
．
两名学生参加考试，随机变量x代表通过的学生数，其分布列为
x012
p
1
3
1
2
1
6
那么这两人通过考试的概率最小值为（　　）
A、
1
6
B、
1
3
C、
1
2
D、
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网