题目内容
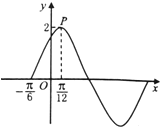 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,| π |
| 2 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)已知α∈(π,
| 3π |
| 2 |
| α |
| 2 |
| 5π |
| 12 |
| 6 |
| 5 |
| α |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)由图象可得A=2,由周期可得ω,代点可解φ,可得解析式;(Ⅱ)由题意易得cosα=-
,可得sinα=-
,而f(
)=sinα+
cosα,代入化简即可.
| 3 |
| 5 |
| 4 |
| 5 |
| α |
| 2 |
| 3 |
解答:
解:(Ⅰ)由图象结合题意可知A=2,又图象过点(-
,0)和(
,2)
∴
•
=
-(-
),解得ω=2,
∴2sin(-
×2+φ)=0,结合φ∈(0,
)可得φ=
,
∴f(x)=2sin(2x+
);
(Ⅱ)由(Ⅰ)知f(
-
)=2sin(α-
)=
,
∴sin(α-
)=-cosα=
,∴cosα=-
,
又∵α∈(π,
),∴sinα=-
,
∴f(
)=2sin(α+
)=sinα+
cosα
=-
-
=-
.
| π |
| 6 |
| π |
| 12 |
∴
| 1 |
| 4 |
| 2π |
| ω |
| π |
| 12 |
| π |
| 6 |
∴2sin(-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∴f(x)=2sin(2x+
| π |
| 3 |
(Ⅱ)由(Ⅰ)知f(
| α |
| 2 |
| 5π |
| 12 |
| π |
| 2 |
| 6 |
| 5 |
∴sin(α-
| π |
| 2 |
| 3 |
| 5 |
| 3 |
| 5 |
又∵α∈(π,
| 3π |
| 2 |
| 4 |
| 5 |
∴f(
| α |
| 2 |
| π |
| 3 |
| 3 |
=-
| 4 |
| 5 |
| 3 |
| 5 |
| 3 |
4+3
| ||
| 5 |
点评:本题考查三角函数解析式的求解,涉及三角函数公式的应用,属中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 如图,一个底面半径为
如图,一个底面半径为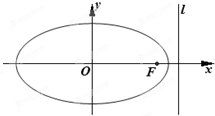 椭圆C的右焦点为F,右准线为l,离心率为
椭圆C的右焦点为F,右准线为l,离心率为