题目内容
8.已知实数x,y满足$\left\{\begin{array}{l}3x-2y-3≤0\\ x-3y+6≥0\\ 2x+y-2≥0\end{array}\right.$,在这两个实数x,y之间插入三个实数,使这五个数构成等差数列,那么这个等差数列后三项和的最大值为9.分析 利用数列的关系推出三项和关于x,y的表达式,画出约束条件的可行域,利用线性规划知识求解最值.
解答 解:设构成等差数列的五个数分别为x,a,b,c,y,
因为等差数列的公差$d=\frac{y-x}{4}$,
则$b+c+y=(x+2×\frac{y-x}{4})+(x+3×\frac{y-x}{4})+y=\frac{3}{4}(x+3y)$
(另解:因为由等差数列的性质有x+y=a+c=2b,
所以$b=\frac{x+y}{2},c=\frac{b+y}{2}=\frac{{\frac{x+y}{2}+y}}{2}$.)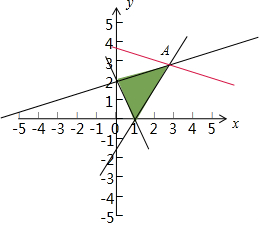
则等差数列后三项和为
$b+c+y=\frac{x+y}{2}+\frac{{\frac{x+y}{2}+y}}{2}+y$=$\frac{3}{4}x+\frac{9}{4}y$
=$\frac{3}{4}(x+3y)$.).
所以设z=x+3y,实数x,y满足$\left\{\begin{array}{l}3x-2y-3≤0\\ x-3y+6≥0\\ 2x+y-2≥0\end{array}\right.$,
作出约束条件所表示的可行域如图所示:
可知当经过点A(3,3)时,
目标函数z=x+3y有最大值12,此时b+c+y有最大值9.
故答案为:9.
点评 本题考查数列以及线性规划的简单应用,考查数形结合以及计算能力.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
20.为了得到函数$y=cos(2x-\frac{π}{2})$的图象,可以将函数y=cos2x的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向左平移$\frac{π}{4}$个单位长度 | ||
| C. | 向右平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
3.某空间几何体的三视图如图所示(图中小正方形的边长为1),则这个几何体的体积是( )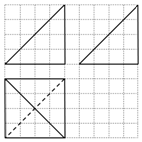

| A. | $\frac{32}{3}$ | B. | $\frac{64}{3}$ | C. | 16 | D. | 32 |
19.执行如图所示的程序框图,输出S的值为( )
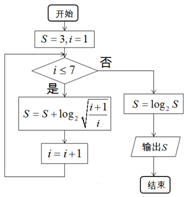

| A. | log210-1 | B. | 2log23-1 | C. | $\frac{9}{2}$ | D. | 6 |
 ,且
,且 ,则
,则 的值是 ( )
的值是 ( ) C.
C. D.400
D.400