题目内容
16.函数$f(x)=\frac{ax+b}{{{x^2}+1}}$是定义在(-∞,+∞)上的奇函数,且$f(\frac{1}{2})=\frac{2}{5}$.(1)求函数f(x)的解析式;
(2)判断f(x)在区间(-1,1)上的单调性,并用定义证明你的结论.
分析 (1)利用奇函数的定义,及特殊点,求函数f(x)的解析式;
(2)利用函数的单调性的定义证明求解即可.
解答 解:(1)∵f(x)是奇函数,∴f(-x)=-f(x).
即$\frac{-ax+b}{{{x^2}+1}}=-\frac{ax+b}{{{x^2}+1}}$,-ax+b=-ax-b,∴b=0.
∴$f(x)=\frac{ax}{{{x^2}+1}}$,又$f(\frac{1}{2})=\frac{2}{5}$,∴$\frac{{\frac{1}{2}a}}{{\frac{1}{4}+1}}=\frac{2}{5}$,∴a=1,
∴$f(x)=\frac{x}{{{x^2}+1}}$.
(2)任取x1,x2∈(-1,1),且x1<x2,
$f({x_1})-f({x_2})=\frac{x_1}{{{x_1}^2+1}}-\frac{x_2}{{{x_2}^2+1}}=\frac{{({x_1}-{x_2})(1-{x_1}{x_2})}}{{({x_1}^2+1)({x_2}^2+1)}}$,
∵-1<x1<x2<1,∴-1<x1x2<1,
∴1-x1x2>0,又x1-x2<0,${x_1}^2+1>0$,${x_2}^2+1>0$,
∴f(x1)-f(x2)<0,f(x1)<f(x2),
∴f(x)在区间(-1,1)上是增函数.
点评 本题考查函数的与方程的应用,考查函数的奇偶性以及函数的单调性的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
5.设偶函数f(x)满足f(x)=2x-4(x≥0),则满足f(a-2)>0的实数a的取值范围为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
1.执行如图所示的程序框图,输出S的值为( )


| A. | 6 | B. | 2log23+1 | C. | 2log23+3 | D. | log23+1 |
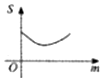
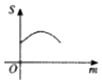
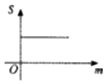
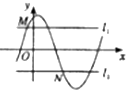 如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )
如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )