题目内容
20.已知曲线C的极坐标方程是ρ=6cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数).(1)将曲线C的极坐标方程化为直角坐标方程(普通方程);
(2)若直线l与曲线C相交于A、B两点,且|AB|=2$\sqrt{7}$,求直线的倾斜角α的值.
分析 (1)利用极坐标与直角坐标的互化方法,可将曲线C的极坐标方程化为直角坐标方程(普通方程);
(2)直线l的参数方程是$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),代入圆的方程,整理可得t2-4tcosα-5=0,利用参数的几何意义,建立方程,即可求直线的倾斜角α的值.
解答 解:(1)曲线C的极坐标方程是ρ=6cosθ,可得ρ2=6ρcosθ,直角坐标方程为x2+y2-6x=0,即(x-3)2+y2=9
(2)直线l的参数方程是$\left\{\begin{array}{l}{x=1+tcosα}\\{y=tsinα}\end{array}\right.$(t为参数),代入圆的方程,整理可得t2-4tcosα-5=0
设A,B对应的参数为t1,t2,则t1+t2=4cosα,t1t2=-5,
∴|AB|=|t1-t2|=$\sqrt{16co{s}^{2}α+20}$=2$\sqrt{7}$,
∴cosα=±$\frac{\sqrt{2}}{2}$,
∵α∈[0,π),
∴α=$\frac{π}{4}$或$\frac{3π}{4}$.
点评 本题考查极坐标化为直角坐标,考查参数方程的运用,考查参数的几何意义,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11.若复数$\frac{1+ai}{2-i}$(a∈R)的实部和虚部相等,则实数a的值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
15.在△ABC中,a,b,c分别为内角A,B,C所对的边,且满足b=c,$\frac{b}{a}$=$\frac{1-cosB}{cosA}$,若点O是△ABC外一点,∠AOB=θ(0<θ<π),OA=2,OB=1,则平面四边形OACB面积的最大值是( )
| A. | $\frac{4+5\sqrt{3}}{4}$ | B. | $\frac{8+5\sqrt{3}}{4}$ | C. | 3 | D. | $\frac{4+\sqrt{5}}{2}$ |
5.设偶函数f(x)满足f(x)=2x-4(x≥0),则满足f(a-2)>0的实数a的取值范围为( )
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
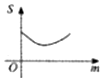
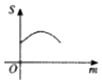
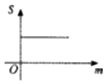
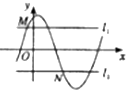 如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )
如图,M(xM,yM),N(xN,yN)分别是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与两条直线l1:y=m(A≥m≥0),l2:y=-m的两个交点,记S(m)=|xM-xN|,则S(m)的图象大致是( )