题目内容
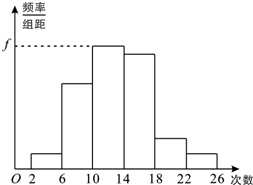 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:| 组别 | 锻炼次数 | 频数(人) | 频率 |
| 1 | [2,6) | 2 | 0.04 |
| 2 | [6,10) | 11 | 0.22 |
| 3 | [10,14) | 16 | c |
| 4 | [14,18) | 15 | 0.30 |
| 5 | [18,22) | d | e |
| 6 | [22,26) | 2 | 0.04 |
| 合计 | M | 1.00 |
(Ⅱ)求参加锻炼次数的众数(直接写出答案,不要求计算过程);
(Ⅲ)从参加锻炼次数不少于18次的学生中任选2人,求至少一人参加锻炼的次数在区间[22,26]内的概率.
考点:古典概型及其概率计算公式,频率分布直方图
专题:计算题,概率与统计
分析:(I)利用
=频率,求得M;再求得d,c的值;
(II)根据众数是最高小矩形底边中点的横坐标求解;
(III)用列举法写出从6人中任取2人的所有基本事件,找出至少一人参加锻炼的次数在区间[22,26)内的基本事件,利用个数比求概率.
| 频数 |
| 样本容量 |
(II)根据众数是最高小矩形底边中点的横坐标求解;
(III)用列举法写出从6人中任取2人的所有基本事件,找出至少一人参加锻炼的次数在区间[22,26)内的基本事件,利用个数比求概率.
解答:
解:(I)∵
=0.04,∴M=50,
又2+11+16+15+d+2=M,∴d=4;
又∵c=
=0.32,∴f=
=0.08;
(II)∵第三组的小矩形最高,∴众数为从左数第三个小矩形底边中点的横坐标,∴众数为12;
(III)参加次数不少于18次的学生共有:4+2=6人
设在[18,22)内的4人为:A、B、C、D,在[22,26)内的2人为m、n,
在这6人中任取2人共有:AB、AC、AD、Am、An、BC、BD、Bm、Bn、CD、Cm、Cn、Dm、Dn、mn共15种,
其中至少一人参加锻炼的次数在区间[22,26)内Am、An、Bm、Bn、Cm、Cn、Dm、Dn、mn共9种.
∴所求的概率为P=
=
.
| 2 |
| M |
又2+11+16+15+d+2=M,∴d=4;
又∵c=
| 16 |
| 50 |
| 0.32 |
| 4 |
(II)∵第三组的小矩形最高,∴众数为从左数第三个小矩形底边中点的横坐标,∴众数为12;
(III)参加次数不少于18次的学生共有:4+2=6人
设在[18,22)内的4人为:A、B、C、D,在[22,26)内的2人为m、n,
在这6人中任取2人共有:AB、AC、AD、Am、An、BC、BD、Bm、Bn、CD、Cm、Cn、Dm、Dn、mn共15种,
其中至少一人参加锻炼的次数在区间[22,26)内Am、An、Bm、Bn、Cm、Cn、Dm、Dn、mn共9种.
∴所求的概率为P=
| 9 |
| 15 |
| 3 |
| 5 |
点评:本小题主要考查频率分布表、频率分布直方图、众数及中位数、概率等相关基础知识,考查运算求解能力、推理能力,
考查了函数与方程、数形结合、转化与化归的数学思想方法.
考查了函数与方程、数形结合、转化与化归的数学思想方法.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
两个数列{an},{bn}满足
,其中a1=2,b1=0,则a10等于( )
|
| A、310+1 |
| B、210+1 |
| C、39-1 |
| D、29-1 |