题目内容
下表示某地一年中10天测量的白昼时间统计表(时间近似到0.1小时)
(1)以日期在365天中的位置序号x为横坐标,白昼时间y为纵坐标,在给定坐标系中画出这些数据的散点图;
(2)试选用一个形如y=Asin(ωt+φ)+t的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
(3)用(2)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
| 日期 | 1月1日 | 2月28日 | 3月21日 | 4月27日 | 5月6日 | 6月21日 | 8月13日 | 9月20日 | 10月25日 | 12月21日 |
| 日期位置序号x | 1 | 59 | 80 | 117 | 126 | 172 | 225 | 263 | 298 | 355 |
| 白昼时间y(小时) | 5.6 | 10.2 | 12.4 | 16.4 | 17.3 | 19.4 | 16.4 | 12.4 | 8.5 | 5.4 |
(2)试选用一个形如y=Asin(ωt+φ)+t的函数来近似描述一年中白昼时间y与日期位置序号x之间的函数关系.[注:①求出所选用的函数关系式;②一年按365天计算]
(3)用(2)中的函数模型估计该地一年中大约有多少天白昼时间大于15.9小时.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:计算题
分析:(1)按做散点图的要求作图就可以;
(2)由散点图找到最值、周期,然后代入数据求出各参数;.
(3)根据题意列出不等式组,解得答案.
(2)由散点图找到最值、周期,然后代入数据求出各参数;.
(3)根据题意列出不等式组,解得答案.
解答:
解:(1)散点图如图所示:

(2)由散点图知白昼时间与日期序号之间的函数关系式近似y=Asin(ωx+φ)+t,
由图形知函数的最大值为19.4,最小值为5.4,即ymax=19.4,ymin=5.4,
∴A=
=7,t=
=12.4,
又T=365,∴ω=
,
当x=172时,
+φ=
,
∴φ=-
,
∴y=7sin(
x-
)+12.4+12.4,1≤x≤365,x∈N*.
(3)∵y>19.5,
∴7sin(
x-
)+12.4+12.4>15.9,
∴sin(
x-
)+12.4>
,
∴
<
x-
<
π,
∴112≤x≤232,
∴该地区有121(或122)天白昼时间.

(2)由散点图知白昼时间与日期序号之间的函数关系式近似y=Asin(ωx+φ)+t,
由图形知函数的最大值为19.4,最小值为5.4,即ymax=19.4,ymin=5.4,
∴A=
| 19.4-5.4 |
| 2 |
| 19.4+5.4 |
| 2 |
又T=365,∴ω=
| 2π |
| 365 |
当x=172时,
| 2πx |
| 365 |
| π |
| 2 |
∴φ=-
| 323π |
| 730 |
∴y=7sin(
| 2π |
| 365 |
| 323π |
| 730 |
(3)∵y>19.5,
∴7sin(
| 2π |
| 365 |
| 323π |
| 730 |
∴sin(
| 2π |
| 365 |
| 323π |
| 730 |
| 1 |
| 2 |
∴
| π |
| 6 |
| 2π |
| 365 |
| 323π |
| 730 |
| 5 |
| 6 |
∴112≤x≤232,
∴该地区有121(或122)天白昼时间.
点评:本题考查的绘图能力,识图能力,根据图象得到所求的各要素,并注意计算的正确程度.

练习册系列答案
相关题目
已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),且a+2b+3c=0,f(0)•f(1)>0,设x1,x2是方程f(x)=0的两根,则|x1-x2|的取值范围是( )
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
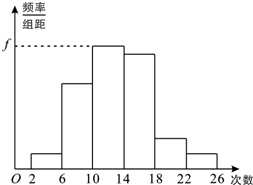 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图: