题目内容
函数f（x）=3xsin（2x+5）的导数是 ．
考点：导数的运算
专题：导数的概念及应用
分析：根据复合函数的导数的运算公式即可得到结论．
解答：
解：∵f（x）=3xsin（2x+5），
∴f'（x）=3sin（2x+5）+3xcos（2x+5）×2=3sin（2x+5）+6cos（2x+5），
故答案为：3sin（2x+5）+6cos（2x+5）
∴f'（x）=3sin（2x+5）+3xcos（2x+5）×2=3sin（2x+5）+6cos（2x+5），
故答案为：3sin（2x+5）+6cos（2x+5）
点评：本题主要考查导数的计算，利用复合函数的导数公式以及导数的运算法则是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知函数g（x）=ax3+bx2+cx+d（a≠0）的导函数为f（x），且a+2b+3c=0，f（0）•f（1）＞0，设x1，x2是方程f（x）=0的两根，则|x1-x2|的取值范围是（ ）
A、[0，
| ||||
B、[0，
| ||||
C、（
| ||||
D、（
|
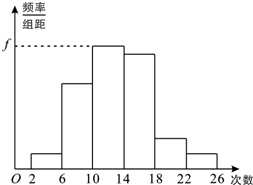为了解某校学生暑期参加体育锻炼的情况，对某班M名学生暑期参加体育锻炼的次数进行了统计，得到如下的频率分布表与直方图：