题目内容
求函数y=log2（x2+2x+3）的单调递增递减区间及值域．
考点：复合函数的单调性
专题：函数的性质及应用
分析：令t=x2+2x+3＞0，求得函数的定义域为R，且y=log2t，根据函数t的增区间和值域，求得函数y的增区间和值域．
解答：
解：令t=x2+2x+3＞0，求得函数的定义域为R，且y=log2t，
∵函数t=（x+1）2+2，
∴函数t的增区间为[-1，+∞），
从而得到函数y的增区间为[-1，+∞）．
再根据t≥2，可得 y≥1，即函数y的值域为[1，+∞）．
∵函数t=（x+1）2+2，
∴函数t的增区间为[-1，+∞），
从而得到函数y的增区间为[-1，+∞）．
再根据t≥2，可得 y≥1，即函数y的值域为[1，+∞）．
点评：本题主要考查复合函数的单调性，求复合函数的值域，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
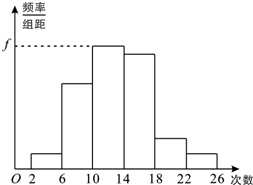为了解某校学生暑期参加体育锻炼的情况，对某班M名学生暑期参加体育锻炼的次数进行了统计，得到如下的频率分布表与直方图：