题目内容
设函数f(x)=2x+
-1(a为实数),当a=0时,若函数y=g(x)为奇函数,且在x>0时,g(x)=f(x).求函数y=g(x)的解析式.
| a |
| 2x |
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:当a=0时,求出x>0时,g(x)=f(x)的解析式,利用y=g(x)是奇函数,再求出x<0时,g(x)的解析式,即得函数y=g(x)的解析式.
解答:
解:∵函数f(x)=2x+
-1(a为实数),
∴当a=0时,f(x)=2x-1;
又∵x>0时,g(x)=f(x)=2x-1,
∴当x<0时,-x>0,
∴g(-x)=2-x-1;
又∵函数y=g(x)为奇函数,
∴g(x)=-g(-x)=-2-x+1;
∴函数y=g(x)=
.
| a |
| 2x |
∴当a=0时,f(x)=2x-1;
又∵x>0时,g(x)=f(x)=2x-1,
∴当x<0时,-x>0,
∴g(-x)=2-x-1;
又∵函数y=g(x)为奇函数,
∴g(x)=-g(-x)=-2-x+1;
∴函数y=g(x)=
|
点评:本题考查了利用函数的奇偶性求函数解析式的问题,解题时应结合函数奇偶性的性质,求出函数的解析式来,是基础题.

练习册系列答案
相关题目
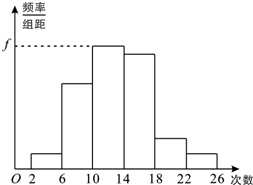 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图: