题目内容
两个数列{an},{bn}满足
,其中a1=2,b1=0,则a10等于( )
|
| A、310+1 |
| B、210+1 |
| C、39-1 |
| D、29-1 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:把bn=an+1-an代入bn+1=4an+bn,然后结合bn+1=an+2-an+1得到an+2+an+1=3(an+1+an),说明
∴{an+1+an}构成以4为首项,以3为公比的等比数列,求出an+1+an=4•3n-1,依次取n=2,3,4,…可以得到a10=4×38-4×37+4×36-4×35+4×34-4×33+4×32-4×3+2,相邻两项合并后利用等比数列求和得到a10的值.
∴{an+1+an}构成以4为首项,以3为公比的等比数列,求出an+1+an=4•3n-1,依次取n=2,3,4,…可以得到a10=4×38-4×37+4×36-4×35+4×34-4×33+4×32-4×3+2,相邻两项合并后利用等比数列求和得到a10的值.
解答:
解:∵
,
由①得:bn=an+1-an ③,
把③代入②得:bn+1=4an+an+1-an=an+1+3an,
再由③得,bn+1=an+2-an+1,
∴an+2-an+1=an+1+3an,
整理得:an+2=2an+1+3an,
即an+2+an+1=3(an+1+an),
∵a1=2,b1=0,
∴a2=a1+b1=2,
∴a2+a1=4≠0,
则
=3,
∴{an+1+an}构成以4为首项,以3为公比的等比数列,
∴an+1+an=4•3n-1,
则a3=4×3-2,
a4=4×32-4×3+2,
a5=4×33-4×32+4×3-2,
…
a10=4×38-4×37+4×36-4×35+4×34-4×33+4×32-4×3+2
=8×37+8×35+8×33+8×3+3-1
=8(37+35+33+3)+3-1
=8×
+3-1
=39-1.
故选:C.
|
由①得:bn=an+1-an ③,
把③代入②得:bn+1=4an+an+1-an=an+1+3an,
再由③得,bn+1=an+2-an+1,
∴an+2-an+1=an+1+3an,
整理得:an+2=2an+1+3an,
即an+2+an+1=3(an+1+an),
∵a1=2,b1=0,
∴a2=a1+b1=2,
∴a2+a1=4≠0,
则
| an+2+an+1 |
| an+1+an |
∴{an+1+an}构成以4为首项,以3为公比的等比数列,
∴an+1+an=4•3n-1,
则a3=4×3-2,
a4=4×32-4×3+2,
a5=4×33-4×32+4×3-2,
…
a10=4×38-4×37+4×36-4×35+4×34-4×33+4×32-4×3+2
=8×37+8×35+8×33+8×3+3-1
=8(37+35+33+3)+3-1
=8×
| 3(1-94) |
| 1-9 |
=39-1.
故选:C.
点评:本题考查数列递推式,解答的关键是化两个数列的递推式为一个数列{an}的二阶递推式,是中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
已知函数g(x)=ax3+bx2+cx+d(a≠0)的导函数为f(x),且a+2b+3c=0,f(0)•f(1)>0,设x1,x2是方程f(x)=0的两根,则|x1-x2|的取值范围是( )
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
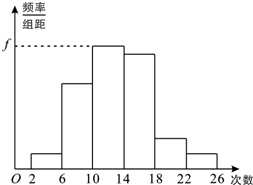 为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图:
为了解某校学生暑期参加体育锻炼的情况,对某班M名学生暑期参加体育锻炼的次数进行了统计,得到如下的频率分布表与直方图: