题目内容
1．直线l与抛物线C：y2=2x交于A，B两点，O为坐标原点，若直线OA，OB的斜率k1，k2满足${k_1}{k_2}=\frac{2}{3}$，则l的横截距（ ）| A． | 为定值-3 | B． | 为定值3 | C． | 为定值-1 | D． | 不是定值 |
分析 直线l：x=my+b，代入抛物线方程可化为y2-2my-2b=0，y1y2=-2b，结合${k_1}{k_2}=\frac{2}{3}$，即可得出结论．
解答 解：设A（x1，y1），B（x2，y2），则$\frac{{y}_{1}}{{x}_{1}}•\frac{{y}_{2}}{{x}_{2}}$=$\frac{2}{3}$．
∴$\frac{{y}_{1}{y}_{2}}{\frac{{{y}_{1}}^{2}{{y}_{2}}^{2}}{4}}$=$\frac{2}{3}$，
∴y1y2=6，
直线l：x=my+b，代入抛物线方程可化为y2-2my-2b=0，
∴y1y2=-2b，
∴-2b=6，∴b=-3，
∴l的横截距为-3
故选：A．
点评 本题考查抛物线方程，考查直线与抛物线的位置关系，比较基础．
练习册系列答案
相关题目
16．
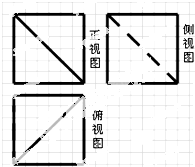如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）| A． | 54 | B． | 162 | C． | 54+18$\sqrt{3}$ | D． | 162+18$\sqrt{3}$ |
6．已知几何体的三视图如图所示，则该几何体的体积为（ ）
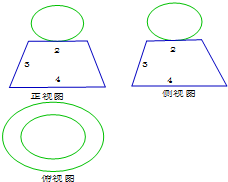
| A． | $\frac{π}{3}（4+14\sqrt{2}）$ | B． | $\frac{{14\sqrt{2}π}}{3}$ | C． | $\frac{5π}{3}$ | D． | $\frac{4π}{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，$CD=2AB=2BP=\sqrt{2}AD$，$\overrightarrow{CE}=λ\overrightarrow{EB}$（λ＞0），DE⊥平面PBC，侧面ABP⊥底面ABCD