题目内容
6．已知几何体的三视图如图所示，则该几何体的体积为（ ）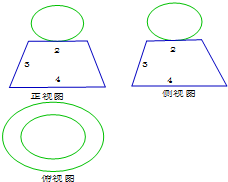
| A． | $\frac{π}{3}（4+14\sqrt{2}）$ | B． | $\frac{{14\sqrt{2}π}}{3}$ | C． | $\frac{5π}{3}$ | D． | $\frac{4π}{3}$ |
分析 由三视图可知：该几何体是由一个球与一个圆台构成的．利用体积计算公式即可得出．
解答 解：由三视图可知：该几何体是由一个球与一个圆台构成的．
该几何体的体积V=$\frac{4π}{3}×{1}^{3}$+$\frac{1}{3}π×（{1}^{2}+{2}^{2}+2）×2\sqrt{2}$=$\frac{π}{3}（4+14\sqrt{2}）$．
故选：A．
点评 本题考查了球与圆台的三视图与体积计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
应用题作业本系列答案
相关题目
14．设抛物线y2=8x的焦点为F，P是抛物线上一点，若直线PF的倾斜角为120°，则|PF|=（ ）
| A． | $\frac{8}{3}$ | B． | 3 | C． | $\frac{8}{3}$或8 | D． | 3或8 |
1．直线l与抛物线C：y2=2x交于A，B两点，O为坐标原点，若直线OA，OB的斜率k1，k2满足${k_1}{k_2}=\frac{2}{3}$，则l的横截距（ ）
| A． | 为定值-3 | B． | 为定值3 | C． | 为定值-1 | D． | 不是定值 |
13．已知某几何体的三视图如图所示，则此几何体的体积是（ ）
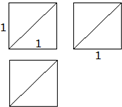
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{5}{6}$ |