题目内容
8.已知高与底面半径相等的圆锥的体积为$\frac{8π}{3}$,其侧面积与球O的表面积相等,则球O的体积为$\frac{{4\root{4}{8}π}}{3}$.分析 利用高与底面半径相等的圆锥的体积为$\frac{8π}{3}$,其侧面积与球O的表面积相等,求出球的半径,即可求出球O的体积.
解答 解:设底面半径为r,球的半径为R,则圆锥的体积为$\frac{1}{3}•π{r}^{2}•r$=$\frac{8π}{3}$,∴r=2,
∵侧面积与球O的表面积相等,
∴$π•r•\sqrt{2}r=4π{R}^{2}$,
∴R=$\frac{\root{4}{2}}{2}$
∴球O的体积V=$\frac{{4\root{4}{8}π}}{3}$.
故答案为$\frac{{4\root{4}{8}π}}{3}$.
点评 本题考查球O的体积,考查学生的计算能力,正确求出球的半径是关键.

练习册系列答案
相关题目
1.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足${k_1}{k_2}=\frac{2}{3}$,则l的横截距( )
| A. | 为定值-3 | B. | 为定值3 | C. | 为定值-1 | D. | 不是定值 |
13.已知某几何体的三视图如图所示,则此几何体的体积是( )
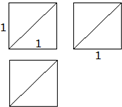

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
17.一个正三棱柱的主(正)视图是长为2$\sqrt{3}$,宽为4的矩形,则它的外接球的表面积等于( )
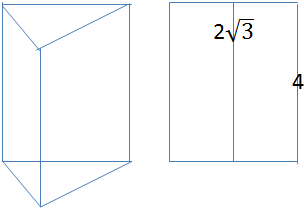

| A. | 64π | B. | 48π | C. | 32π | D. | 16π |
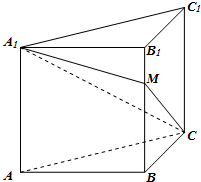 正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M. ,集合
,集合 ,则( )
,则( ) B.
B.
 D.
D.