题目内容
12.定义在R上的函数f(x)满足f(1)=1,且2f′(x)<1,当x∈[0,2π]时,不等式f(2cosx)<2cos2$\frac{x}{2}$-$\frac{1}{2}$的解集为$[{0,\frac{π}{3}})∪({\frac{5π}{3},2π}]$.分析 设g(x)=f(x)-$\frac{1}{2}$x,可得g(x)在R上递减,求出g(1),运用二倍角余弦公式,将原不等式化为f(2cosx)-cosx<$\frac{1}{2}$,即g(2cosx)<g(1),由单调性可得2cosx<1,解不等式即可得到所求范围.
解答 解:设$g(x)=f(x)-\frac{1}{2}x,g'(x)=f'(x)-\frac{1}{2}<0$,$g(1)=f(1)-\frac{1}{2}=\frac{1}{2}$,
不等式$f({2cosx})<2{cos^2}\frac{x}{2}-\frac{1}{2}$,
可化为$f({2cosx})-cosx<\frac{1}{2},即g({2cosx})<g(1)$,
由于$g(x)单调递减,2cosx>1,即cosx>\frac{1}{2}$,
当x∈[0,2π]时,
∴$x∈[{0,\frac{π}{3}})∪({\frac{5π}{3},2π}]$.
故答案为:$[{0,\frac{π}{3}})∪({\frac{5π}{3},2π}]$.
点评 本题考查导数的运用:判断单调性,考查构造函数法和运用单调性解不等式,考查运算能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
4.函数f(x)=lnx2-2的零点是( )
| A. | e | B. | $\sqrt{e}$ | C. | -e | D. | e或-e |
1.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足${k_1}{k_2}=\frac{2}{3}$,则l的横截距( )
| A. | 为定值-3 | B. | 为定值3 | C. | 为定值-1 | D. | 不是定值 |
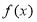 是定义在
是定义在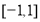 上的奇函数且
上的奇函数且 ,当
,当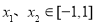 ,且
,且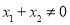 时,有
时,有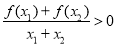 ,若
,若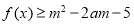 对所有
对所有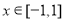 、
、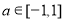 恒成立,则实数
恒成立,则实数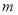 的取值范围是________.
的取值范围是________.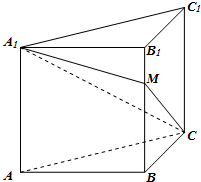 正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.