题目内容
13.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的右焦点为F(1,0),且点$P(1,\frac{3}{2})$在椭圆C上,O为坐标原点.(1)求椭圆C的标准方程;
(2)过椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{{{b^2}-\frac{5}{3}}}$=1上异于其顶点的任一点P,作圆O:x2+y2=$\frac{4}{3}$的两条切线,切点分别为M,N(M,N不在坐标轴上),若直线MN在x轴、y轴上的截距分别为m、n,证明:$\frac{1}{{3{m^2}}}+\frac{1}{n^2}$为定值.
分析 (1)由题意可得c=1,将P代入椭圆方程,解方程可得a,b,进而得到椭圆方程;
(2)由题意:C1:$\frac{x^2}{4}+\frac{{3{y^2}}}{4}=1$,设点P(x1,y1),M(x2,y2),N(x3,y3),求出PM,PN方程,求得直线MN方程,求出MN在x轴、y轴上的截距分别为m、n,结合椭圆方程,即可得到定值.
解答 解:(1)由题意得:c=1,所以a2=b2+1,
又因为点$P(1,\frac{3}{2})$在椭圆C上,所以$\frac{1}{a^2}+\frac{9}{{4{b^2}}}=1$,
可解得a2=4,b2=3,
所以椭圆标准方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)证明:由题意:C1:$\frac{x^2}{4}+\frac{{3{y^2}}}{4}=1$,
设点P(x1,y1),M(x2,y2),N(x3,y3),
因为M,N不在坐标轴上,所以${k_{PM}}=-\frac{1}{{{k_{OM}}}}=-\frac{x_2}{y_2}$,
直线PM的方程为$y-{y_2}=-\frac{x_2}{y_2}(x-{x_2})$,
化简得:${x_2}x+{y_2}y=\frac{4}{3}$--------------④
同理可得直线PN的方程为${x_3}x+{y_3}y=\frac{4}{3}$---------------⑤
把P点的坐标代入④、⑤得$\left\{\begin{array}{l}{x_2}{x_1}+{y_2}{y_1}=\frac{4}{3}\\{x_3}{x_1}+{y_3}{y_1}=\frac{4}{3}\end{array}\right.$,
所以直线MN的方程为${x_1}x+{y_1}y=\frac{4}{3}$,
令y=0,得$m=\frac{4}{{3{x_1}}}$,令x=0得$n=\frac{4}{{3{y_1}}}$,
所以${x_1}=\frac{4}{3m}$,${y_1}=\frac{4}{3n}$,又点P在椭圆C1上,
所以${(\frac{4}{3m})^2}+3{(\frac{4}{3n})^2}=4$,
即$\frac{1}{{3{m^2}}}+\frac{1}{n^2}=\frac{3}{4}$为定值.
点评 本题考查椭圆方程的求法,注意运用点满足椭圆方程,考查定值的证明,注意运用圆上一点的切线方程,考查直线方程运用,考查化简整理的运算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 为定值-3 | B. | 为定值3 | C. | 为定值-1 | D. | 不是定值 |
 根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.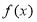 是定义在
是定义在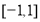 上的奇函数且
上的奇函数且 ,当
,当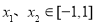 ,且
,且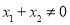 时,有
时,有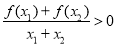 ,若
,若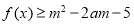 对所有
对所有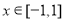 、
、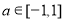 恒成立,则实数
恒成立,则实数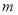 的取值范围是________.
的取值范围是________.