题目内容
16.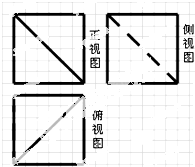 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )| A. | 54 | B. | 162 | C. | 54+18$\sqrt{3}$ | D. | 162+18$\sqrt{3}$ |
分析 由已知中的三视图可得:该几何体是一个正方体截去一个三棱锥得到的组合体,其表面有三个边长为6的正方形,三个直角边长为6的等腰直角三角形,和一个边长为6$\sqrt{2}$的等边三角形组成,累加各个面的面积可得答案.
解答 解:由已知中的三视图可得:该几何体是一个正方体截去一个三棱锥得到的组合体,
其表面有三个边长为6的正方形,三个直角边长为6的等腰直角三角形,和一个边长为6$\sqrt{2}$的等边三角形组成,
故表面积S=3×6×6+3×$\frac{1}{2}$×6×6+$\frac{\sqrt{3}}{4}$×$(6\sqrt{2})^{2}$=162+18$\sqrt{3}$,
故选:D
点评 本题考查的知识点是棱锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
4.函数f(x)=lnx2-2的零点是( )
| A. | e | B. | $\sqrt{e}$ | C. | -e | D. | e或-e |
1.直线l与抛物线C:y2=2x交于A,B两点,O为坐标原点,若直线OA,OB的斜率k1,k2满足${k_1}{k_2}=\frac{2}{3}$,则l的横截距( )
| A. | 为定值-3 | B. | 为定值3 | C. | 为定值-1 | D. | 不是定值 |
 根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图. S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).
S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).