题目内容
14.已知数列{an}中,a1=-2,a2=3且$\frac{{a}_{n+2}-3{a}_{n+1}}{{a}_{n+1}-3{a}_{n}}$=3,则数列{an}的前n项和Sn=$\frac{13+(6n-13)•{3}^{n}}{4}$.分析 根据数列的通项公式求出数列的通项公式,再根据错位相减法求和即可,
解答 解:∵a1=-2,a2=3且$\frac{{a}_{n+2}-3{a}_{n+1}}{{a}_{n+1}-3{a}_{n}}$=3,
∴$\frac{{a}_{3}-3{a}_{2}}{{a}_{2}-3{a}_{1}}$=3,$\frac{{a}_{4}-3{a}_{3}}{{a}_{3}-3{a}_{2}}$=3,$\frac{{a}_{5}-3{a}_{4}}{{a}_{4}-3{a}_{3}}$=3,…,$\frac{{a}_{n+2}-3{a}_{n+1}}{{a}_{n+1}-3{a}_{n}}$=3,
累乘可得$\frac{{a}_{n+2}-3{a}_{n+1}}{{a}_{2}-3{a}_{1}}$=3n,
∵a2-3a1=3-3×(-2)=9,
∴an+2-3an+1=3n+2,
∴$\frac{{a}_{n+2}}{{3}^{n+2}}$-$\frac{{a}_{n+1}}{{3}^{n+1}}$=1,
即数列{$\frac{{a}_{n+1}}{{3}^{n+1}}$}为等差数列,
∴$\frac{{a}_{n+1}}{{3}^{n+1}}$=$\frac{1}{3}$+n-1=n-$\frac{2}{3}$,
∴an+1=(n-$\frac{2}{3}$)•3n+1,
∵a1=-2也满足上式,
∴an=(n-$\frac{5}{3}$)•3n=(3n-5)•3n-1,
∴Sn=-2•30+1•31+4•32+…+(3n-5)•3n-1,
∴3Sn=-2•31+1•32+4•33+…+(3n-5)•3n,
∴-2Sn=-2+3(31+32+33+…+3n-1)-(3n-5)•3n=-2+$\frac{9×(1-{3}^{n-1})}{1-3}$-(3n-5)•3n,
∴Sn=$\frac{13+(6n-13)•{3}^{n}}{4}$,
故答案为:Sn=$\frac{13+(6n-13)•{3}^{n}}{4}$
点评 本题考查了数列的递推公式求通项公式和错位想减法求前n项和,考查了学生的运算能力和转化能力,属于中档题.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
| A. | $\frac{2}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
| A. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$](k∈Z) | B. | [kπ,kπ+$\frac{π}{2}$](k∈Z) | C. | [kπ-$\frac{π}{6}$,kπ+$\frac{2π}{3}$](k∈Z) | D. | [kπ-$\frac{π}{2}$,kπ](k∈Z) |
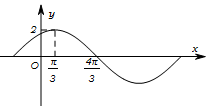 已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示. ,∠C=
,∠C= ,则∠A=_______.
,则∠A=_______.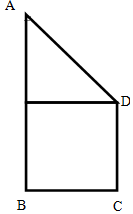 已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积.
已知四边形ABCD为直角梯形,AB∥CD,AB=4,BC=CD=2,AB⊥BC,现将该梯形绕AB所在直线旋转一周,得到一个封闭的几何体,求该几何体的表面积及体积.