题目内容
9.已知a,b∈R,且ex≥a(x-1)+b对x∈R恒成立,则ab的最大值是( )| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
分析 先求出函数的导数,再分别讨论a=0,a<0,a>0的情况,从而得出ab的最大值.
解答 解:令f(x)=ex-a(x-1)-b,则f′(x)=ex-a,
若a=0,则f(x)=ex-b≥-b≥0,得b≤0,此时ab=0;
若a<0,则f′(x)>0,函数单调增,x→-∞,此时f(x)→-∞,不可能恒有f(x)≥0.
若a>0,由f′(x)=ex-a=0,得极小值点x=lna,
由f(lna)=a-alna+a-b≥0,得b≤a(2-lna),
ab≤a2(2-lna).
令g(a)=a2(2-lna).
则g′(a)=2a(2-lna)-a=a(3-2lna)=0,得极大值点a=${e}^{\frac{3}{2}}$.
而g(${e}^{\frac{3}{2}}$)=$\frac{1}{2}{e}^{3}$.
∴ab的最大值是$\frac{1}{2}{e}^{3}$.
故选:A.
点评 本题考查函数恒成立问题,考查了函数的单调性,训练了导数在求最值中的应用,渗透了分类讨论思想,是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
2.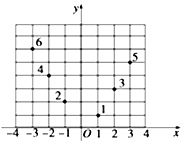 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\{{a_n}\}(n∈{N^*})$的前12项,其中横坐标为奇数项,纵坐标为偶数项,按如此规律下去,则a2017+a2018+a2019等于( )| A. | 1002 | B. | 1004 | C. | 1007 | D. | 1009 |
1.若f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x-1)}}$,则f(x+1)的定义域为( )
| A. | (-$\frac{1}{2}$,0) | B. | (-$\frac{1}{2}$,0] | C. | (-$\frac{1}{2}$,+∞) | D. | (0,+∞) |
18.下列说法正确的是( )
| A. | 函数的极大值就是函数的最大值 | |
| B. | 函数的极小值就是函数的最小值 | |
| C. | 函数的最值一定是极值 | |
| D. | 闭区间上的连续函数一定存在最大值与最小值 |
18.已知函数f(x)=$\frac{1}{2}$ax2+bx+1,其中a∈{2,4},b∈{1,3},从f(x)中随机抽取1个,则它在(-∞,-1]上是减函数的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |