题目内容
7.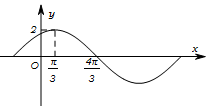 已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ).($A>0,ω>0,0<φ<\frac{π}{2}$)的部分图象如图所示.(1)求函数f(x)的解析式;
(2)若$f({2α+\frac{π}{3}})=\frac{{\sqrt{10}}}{5}$,且α∈(0,π),求tanα的值.
分析 (1)根据图象求出A,ω 和φ,即可求函数f(x)的解析式;
(2)根据函数解析式之间的关系即可得到结论.
解答 解:(1)由题设图象知,周期T=4($\frac{4π}{3}-\frac{π}{3}$)=4π,
∴ω=$\frac{2π}{T}$=$\frac{1}{2}$.
∵点($\frac{4π}{3}$,0)在函数图象上,
∴Asin($\frac{1}{2}×\frac{4π}{3}$+φ)=0,即sin($\frac{2π}{3}$+φ)=0.
又∵0<φ<$\frac{π}{2}$,
∴φ=$\frac{π}{3}$.
又点($\frac{π}{3}$,2)在函数图象上,
∴Asin$\frac{π}{3}×\frac{1}{2}+\frac{π}{3}$=2,即A=2.
故函数f(x)的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{π}{3}$)
(2)若$f({2α+\frac{π}{3}})=\frac{{\sqrt{10}}}{5}$,即2sin(α+$\frac{π}{6}$$+\frac{π}{3}$)=$\frac{\sqrt{10}}{5}$
可得:2cosα=$\frac{\sqrt{10}}{5}$,即cosα=$\frac{\sqrt{10}}{10}$
α∈(0,π),
∴sinα=$\frac{3\sqrt{10}}{10}$.
则tanα=$\frac{sinα}{cosα}$=3.
点评 本题主要考查三角函数的图象和性质,根据图象求出函数的解析式是解决本题的关键.要求熟练掌握函数图象之间的变化关系

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.设an=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{{n}^{2}}$(n∈N*),则a2=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
20.已知$cosθ=-\frac{3}{5}$,$tanθ=\frac{4}{3}$,则角θ的终边落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |