题目内容
6.下列函数中,既是偶函数,又在(0,π)上递增的函数的个数是( )①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由条件,利用三角函数的奇偶性和单调性,得出结论.
解答 解:由于下列函数中,对于函数①y=tan|x|,当x=$\frac{π}{2}$时,函数无意义,故①不满足条件.
对于②y=cos(-x)=cosx为偶函数,且在(0,π)上递减,故②不满足条件.
对于③$y=sin({x-\frac{π}{2}})$=-cosx 为偶函数,且在(0,π)上递增,故③满足条件.
当x∈(0,π)时,$\frac{x}{2}$∈(0,$\frac{π}{2}$),tan$\frac{x}{2}$单调递增,
故$y=|{cot\frac{x}{2}}|$=$\frac{1}{|tan\frac{x}{2}|}$是偶函数,且在(0,π)上递减,故④不满足条件,
故选:A.
点评 本题主要考查三角函数的奇偶性和单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.函数f(x)=x3+x-3的零点落在的区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
17.判断下列各组中的两个函数是同一函数的为( )
| A. | ${y_1}=\frac{(x+3)(x-5)}{x+3},{y_2}=x-5$ | B. | y1=$\sqrt{x+1}$•$\sqrt{x-1}$,y2=$\sqrt{(x+1)(x-1)}$ | ||
| C. | y1=x,y2=$\sqrt{{x}^{2}}$ | D. | y1=$\root{3}{{x}^{4}-{x}^{3}}$,y2=$x\root{3}{x-1}$ |
14.在一个有穷数列每相邻两项之间添加一项,使其等于两相邻项的和,我们把这样的操作叫做该数列的一次“H扩展”.已知数列1,2.第一次“H扩展”后得到1,3,2;第二次“H扩展”后得到1,4,3,5,2.那么第10次“H扩展”后得到的数列的项数为( )
| A. | 1023 | B. | 1025 | C. | 513 | D. | 511 |
16.已知点A的坐标为(2,3),F为抛物线y2=2x的焦点,若点P在抛物线上移动,当|PF|-|PA|取得最大值,则点P的坐标是( )
| A. | (2,2) | B. | ($\sqrt{6}$,3) | C. | (3,$\sqrt{6}$) | D. | ($\frac{9}{2}$,3) |
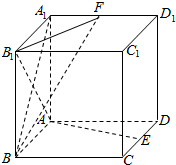 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.