题目内容
17.判断下列各组中的两个函数是同一函数的为( )| A. | ${y_1}=\frac{(x+3)(x-5)}{x+3},{y_2}=x-5$ | B. | y1=$\sqrt{x+1}$•$\sqrt{x-1}$,y2=$\sqrt{(x+1)(x-1)}$ | ||
| C. | y1=x,y2=$\sqrt{{x}^{2}}$ | D. | y1=$\root{3}{{x}^{4}-{x}^{3}}$,y2=$x\root{3}{x-1}$ |
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是同一函数.
解答 解:对于A,函数y1=$\frac{(x+3)(x-5)}{x+3}$=x-5(x≠-3),与y2=x-5(x∈R)的定义域不同,所以不是同一函数;
对于B,函数y1=$\sqrt{x+1}$•$\sqrt{x-1}$=$\sqrt{(x+1)(x-1)}$(x≥1),与y2=$\sqrt{(x+1)(x-1)}$(x≤-1或x≥1)的定义域不同,所以不是同一函数;
对于C,函数y1=x(x∈R),与y2=$\sqrt{{x}^{2}}$=|x|(x∈R)的对应关系不同,所以不是同一函数;
对于D,函数y1=$\root{3}{{x}^{4}{-x}^{3}}$=x$\root{3}{x-1}$(x∈R),与y2=x$\root{3}{x-1}$(x∈R)的定义域相同,对应关系也相同,所以是同一函数.
故选:D.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.

练习册系列答案
相关题目
7.方程kx2+4y2=4k表示焦点在x轴的椭圆,则实数k的取值范围是( )
| A. | k>4 | B. | k=4 | C. | k<4 | D. | 0<k<4 |
8.直线x+y-2=0与直线x-y+3=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 不能确定 |
5.已知ab≠0,点M(a,b)是圆x2+y2=r2内一点,直线l的方程是ax+by=r2,则下列结论正确的是( )
| A. | l与圆相交 | B. | l与圆相切 | C. | l与圆相离 | D. | 不确定 |
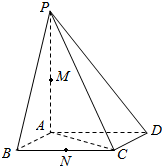 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.