题目内容
16.已知点A的坐标为(2,3),F为抛物线y2=2x的焦点,若点P在抛物线上移动,当|PF|-|PA|取得最大值,则点P的坐标是( )| A. | (2,2) | B. | ($\sqrt{6}$,3) | C. | (3,$\sqrt{6}$) | D. | ($\frac{9}{2}$,3) |
分析 作PM⊥准线l,M为垂足,由抛物线的定义可得|PF|-|PA|=|PM|-|PA|,故当P,A,M三点共线时,|PF|-|PA|最大为|AM|,此时,P点的纵坐标为3,代入抛物线的方程可求得P点的横坐标,从而得到P点的坐标.
解答 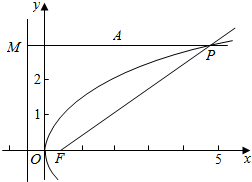 解:由题意可得F($\frac{1}{2}$,0 ),
解:由题意可得F($\frac{1}{2}$,0 ),
准线方程为x=-$\frac{1}{2}$,
作PM⊥准线l,M为垂足,
由抛物线的定义可得|PF|-|PA|=|PM|-|PA|,
故当P,A,M三点共线时,|PF|-|PA|取得最大值,
且为|AM|=2-(-$\frac{1}{2}$)=$\frac{5}{2}$,
此时,P点的纵坐标为3,
代入抛物线的方程可求得P点的横坐标为$\frac{9}{2}$,
故P点的坐标为($\frac{9}{2}$,3),
故选:D.
点评 本题主要考查抛物线的定义、标准方程,以及简单性质的应用,判断当P,A,M三点共线时,|PF|-|PA|最大为|AM|,是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.下列函数中,既是偶函数,又在(0,π)上递增的函数的个数是( )
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.在△ABC中,角A为钝角,AB=3,$\overrightarrow{BC}$•$\overrightarrow{BA}$=12,当角C最大时,△ABC的面积等于( )
| A. | 2 | B. | 3 | C. | 5 | D. | $\frac{15}{2}$ |
9.在复平面上,满足|z-1|=|z+i|(i为虚数单位)的复数z对应的点的轨迹为( )
| A. | 椭圆 | B. | 圆 | C. | 线段 | D. | 直线 |
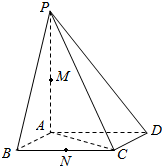 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.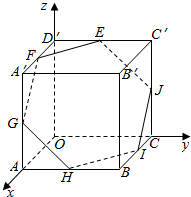 正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.