题目内容
11.已知函数f(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$+x+1,若f(a)+f(a+1)>2,则实数a的取值范围是a>-$\frac{1}{2}$.分析 令g(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$+x+1,得到g(x)的单调性和奇偶性,将f(a)+f(a+1)=g(a)+1+g(a+1)+1>2,转化为g(a)+g(a+1)>0,解出即可.
解答 解:令g(x)=$\frac{{e}^{x}-1}{{e}^{x}+1}$+x+1,则g(-x)=-g(x),是奇函数,
又g′(x)=$\frac{{e}^{x}}{{{(e}^{x}+1)}^{2}}$+1>0,∴g(x)在R上递增,
由f(a)+f(a+1)=g(a)+1+g(a+1)+1>2,
得:g(a)+g(a+1)>0,
∴g(a+1)>-g(a)=g(-a),
∴a+1>-a,解得:a>-$\frac{1}{2}$,
故答案为:a>-$\frac{1}{2}$.
点评 本题考察了函数的单调性和奇偶性问题,考察转化思想,是一道中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
1.$若log_a^{\;}\frac{2}{3}<1,(a>0且a≠1)$,则a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (0,$\frac{2}{3}$)∪(1,+∞) | C. | (1,+∞) | D. | (0,$\frac{2}{3}$)∪($\frac{2}{3}$,+∞) |
6.下列函数中,既是偶函数,又在(0,π)上递增的函数的个数是( )
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.某几何体的三视图如图所示,若此几何体的表面积为(4+2$\sqrt{2}$)π+8,则底面半圆的半径r等于( )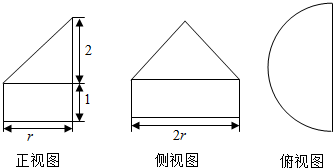

| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
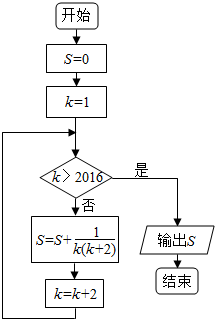
20.执行下列程序框图,则输出结果为( )


| A. | 413 | B. | 404 | C. | 397 | D. | 407 |