题目内容

14．在一个有穷数列每相邻两项之间添加一项，使其等于两相邻项的和，我们把这样的操作叫做该数列的一次“H扩展”．已知数列1，2．第一次“H扩展”后得到1，3，2；第二次“H扩展”后得到1，4，3，5，2．那么第10次“H扩展”后得到的数列的项数为（　　）
A．1023B．1025C．513D．511

分析 化简可得$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=2，从而可得{an-1}是以2为首项，2为公比的等比数列，从而解得．

解答 解：设第n次“H扩展”后得到的数列的项数为an，
则第n+1次“H扩展”后得到的数列的项数为an+1=2an-1，
∴$\frac{{a}_{n+1}-1}{{a}_{n}-1}$=2，
又∵a1-1=3-1=2，
∴{an-1}是以2为首项，2为公比的等比数列，
∴an-1=2•2n-1，
∴an=2n+1，
∴a10=210+1=1025；
故选B．

点评 本题考查了等比数列的性质的判断与应用，关键在于构造等比数列．

练习册系列答案
相关题目
4．若m、n是任意实数，且m＞n，则（　　）
A．m2＞n2B．$\frac{n}{m}＜1$C．lg（m-n）＞0D．${（\frac{1}{2}）^m}＜{（\frac{1}{2}）^n}$
5．已知ab≠0，点M（a，b）是圆x2+y2=r2内一点，直线l的方程是ax+by=r2，则下列结论正确的是（　　）
A．l与圆相交B．l与圆相切C．l与圆相离D．不确定
2．在△ABC中，a，b，c分别是角A，B，C的对边．已知（a2+b2）sin（A-B）=（a2-b2）sin（A+B），试判断该三角形的形状．
9．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$，左、右焦点分别为F1、F2．
（1）若曲线C1：y2=2px（p＞0）的焦点恰是双曲线的右焦点，且交点连线过点F2，则求双曲线离心率．
（2）过双曲线右焦点F2且倾斜角为60°的线段F2M与y轴交于M，与双曲线交于N，已知$\overrightarrow{M{F_2}}=4\overrightarrow{N{F_2}}$，则求该双曲线的离心率；
（3）若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点，则求此双曲线离心率的取值范围；
（4）若离心率$e∈[\sqrt{2}，2]$，令双曲线的两条渐近线构成的角中，以实轴为平分线的角为θ，则求θ的取值范围；
（5）若存在两条直线x=±m与双曲线相交于A，B，C，D，且四边形ABCD为正方形，则求双曲线离心率的取值范围．
19．执行如图所示的流程图，则输出的S的值为$\frac{1008}{2017}$．
6．下列函数中，既是偶函数，又在（0，π）上递增的函数的个数是（　　）
①y=tan|x|
②y=cos（-x）
③$y=sin（{x-\frac{π}{2}}）$
④$y=|{cot\frac{x}{2}}|$．
A．1个B．2个C．3个D．4个
3．某几何体的三视图如图所示，若此几何体的表面积为（4+2$\sqrt{2}$）π+8，则底面半圆的半径r等于（　　）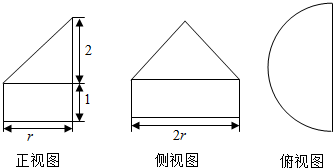
A．1B．$\sqrt{2}$C．2D．2$\sqrt{2}$
4．在△ABC中，角A为钝角，AB=3，$\overrightarrow{BC}$•$\overrightarrow{BA}$=12，当角C最大时，△ABC的面积等于（　　）
A．2B．3C．5D．$\frac{15}{2}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网