题目内容
18.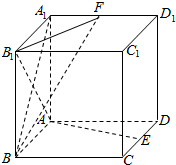 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.(1)求证:AE⊥BF;
(2)求证:平面A1BF⊥平面AB1E;
(3)棱CC1上是否存在点P使AP⊥BF?若存在,确定点P位置;若不存在,说明理由.
分析 (1)取AD中点G,连接FG、BG,通过证明⊥平面BFG,证明AE⊥BF;
(2)连A1B,证明线线垂直,从而证明BF⊥平面AB1E,即可证明平面A1BF⊥平面AB1E;
(3)存在,取CC1中点P,连接EP、C1D,说明AP?平面AB1E,利用BF⊥平面AB1E,推出AP⊥BF.
解答 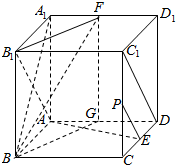 (1)证明:取AD中点G,连接FG、BG,则FG⊥AE,
(1)证明:取AD中点G,连接FG、BG,则FG⊥AE,
又∵△BAG≌△ADE,∴∠ABG=∠DAE,
∴AE⊥BG,又∵BG∩FG=G,
∴AE⊥平面BFG,
∴AE⊥BF;
(2)证明:连A1B,则AB1⊥A1B,
又AB1⊥A1F,A1B∩A1F=A1,
∴AB1⊥平面A1BF,
∴AB1⊥BF,
又AE∩AB1=A,AE⊥BF;
∴BF⊥平面AB1E,
∵BF?平面A1BF,
∴平面A1BF⊥平面AB1E;
(3)解:存在,取CC1中点P,即为所求,
连接EP、C1D
∵EP∥C1D,C1D∥AB1,
∴EP∥AB1,∴AP?平面AB1E,
由(2)知BF⊥平面AB1E,
∴AP⊥BF.
点评 本题考查空间线面、线线垂直的判定及互相转化,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
相关题目
8.直线x+y-2=0与直线x-y+3=0的位置关系是( )
| A. | 平行 | B. | 垂直 | C. | 相交但不垂直 | D. | 不能确定 |
6.下列函数中,既是偶函数,又在(0,π)上递增的函数的个数是( )
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
①y=tan|x|
②y=cos(-x)
③$y=sin({x-\frac{π}{2}})$
④$y=|{cot\frac{x}{2}}|$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.某几何体的三视图如图所示,若此几何体的表面积为(4+2$\sqrt{2}$)π+8,则底面半圆的半径r等于( )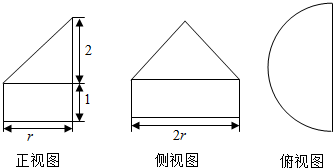

| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
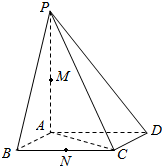 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.